本篇文章主要讲解 RSA 在 CTF 竞赛中的的一些基础题目及数学基础。

题目给出了 e 和 n 以及密文 c,需要求明文 m。
解题思路是根据 n 分解求出 p 和 q,然后根据 e,p,q 求出 d,再根据 c,d,n 求出明文 m。
如何求 p 和 q 呢,这里涉及到质因数的分解,linux下一般可直接执行命令 factor 去分解它:
但是 factor 能分解的数不是很大,当n特别大的时候可以使用 factordb 这个命令 :
1
|
factordb 322831561921859
|
使用下面命令来安装 factordb:
1
|
pip install factordb-pycli
|
当然,我们也可以直接使用在线网站来分解 n:
http://www.factordb.com/index.php
如果 n 特别大,这个网站也分解不出来,那就算了吧。这个题肯定不是分解 n 来解题,一定有别的方法。
本题的解题步骤是先求出 p 和 q:

p 是 13574881 或者 23781539 都行,反正就两个数,你指定第一个是 p 那么第二个就是 q,反之亦可。
解题脚本:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
#!/usr/bin/python
#coding:utf-8
import libnum
from Crypto.Util.number import long_to_bytes
c = 0xdc2eeeb2782c
n = 322831561921859
e = 23
q = 13574881
p = 23781539
d = libnum.invmod(e, (p - 1) *(q - 1))
m = pow(c, d, n)
print "m的值为:"
print long_to_bytes(m)
|
关于 long_to_bytes 与 bytes_to_long 百度一下就知道了,关于如何记住 pow 里面的变量顺序,我记得好像有个 cdn 加速来,靠谐音就记住了。关于求 d,也就是模逆运算,下面的数学基础中会讲。

题目给出了两个文件,如下图所示:
其中 flag.enc 是密文,pubkey.pem 是公钥。正常的话是必须要有私钥才可以解开密文,但是这里加密的强度不高,所以可以直接解开。
现在,我们只知道密文 c,其他的都不知道,怎么办呢?
这里,我们要读取公钥文件 pubkey.pem 中的基本信息。
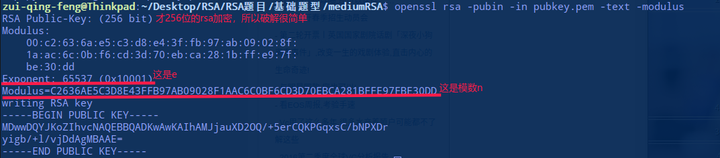
首先把 n 由 16 进制转为 10 进制,接着分解 n 得到 p 和 q。


现在我们有了 n,p,q,e,c。
接着,我们可以根据 p,q 求 phi。然后,再根据 phi 和 e 求 d。最后,根据 c,d,n 即可求出明文 m。
解题脚本:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
#!/usr/bin/python
#coding:utf-8
import libnum
from Crypto.Util.number import long_to_bytes
n = 87924348264132406875276140514499937145050893665602592992418171647042491658461
p = 275127860351348928173285174381581152299
q = 319576316814478949870590164193048041239
e = 65537
phi = (p-1)*(q-1)
d = libnum.invmod(e,phi)
with open('./flag.enc') as f:
c = f.read().encode('hex')
c = int(c,16)
m = pow(c,d,n)
print long_to_bytes(m)
|
或者
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
#!/usr/bin/python
#coding:utf-8
import gmpy2
from Crypto.Util.number import long_to_bytes
n = 87924348264132406875276140514499937145050893665602592992418171647042491658461
p = 275127860351348928173285174381581152299
q = 319576316814478949870590164193048041239
e = 65537
phi = (p-1)*(q-1)
d = gmpy2.invert(e,phi)
with open('./flag.enc') as f:
c = f.read().encode('hex')
c = int(c,16)
m = pow(c,d,n)
print long_to_bytes(m)
|

关于文件形式的密文 c,一般都是 16 进制形式读取,接着再转为整型用于计算。上面的读取代码有点冗余了,后面的题目会有更简洁的读取方式。
真的忘了题目是哪个比赛的题,就叫存货吧。
题目:
1
2
3
4
5
|
p+q : 0x1232fecb92adead91613e7d9ae5e36fe6bb765317d6ed38ad890b4073539a6231a6620584cea5730b5af83a3e80cf30141282c97be4400e33307573af6b25e2ea
(p+1)(q+1) : 0x5248becef1d925d45705a7302700d6a0ffe5877fddf9451a9c1181c4d82365806085fd86fbaab08b6fc66a967b2566d743c626547203b34ea3fdb1bc06dd3bb765fd8b919e3bd2cb15bc175c9498f9d9a0e216c2dde64d81255fa4c05a1ee619fc1fc505285a239e7bc655ec6605d9693078b800ee80931a7a0c84f33c851740
e : 0xe6b1bee47bd63f615c7d0a43c529d219
d : 0x2dde7fbaed477f6d62838d55b0d0964868cf6efb2c282a5f13e6008ce7317a24cb57aec49ef0d738919f47cdcd9677cd52ac2293ec5938aa198f962678b5cd0da344453f521a69b2ac03647cdd8339f4e38cec452d54e60698833d67f9315c02ddaa4c79ebaa902c605d7bda32ce970541b2d9a17d62b52df813b2fb0c5ab1a5
enc_flag: 0x50ae00623211ba6089ddfae21e204ab616f6c9d294e913550af3d66e85d0c0693ed53ed55c46d8cca1d7c2ad44839030df26b70f22a8567171a759b76fe5f07b3c5a6ec89117ed0a36c0950956b9cde880c575737f779143f921d745ac3bb0e379c05d9a3cc6bf0bea8aa91e4d5e752c7eb46b2e023edbc07d24a7c460a34a9a
|
题目给出了 p+q,(p+1)(q+1),e,d,c。
当时做这题的时候就蒙了,n 在哪? p,q 呢? 我是谁? 我在哪? 仔细想了一会,掏出笔记本列了一下等式关系,就出来了…
1
2
3
4
5
6
7
|
(p+1)(q+1)
= p*q + p + q + 1
= n + (p+q) + 1
那么:
n = (p+1)(q+1) - (p+q) - 1
m = pow(c,d,n)
|
解题脚本:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
#!/usr/bin/python
#coding:utf-8
import gmpy2
from Crypto.Util.number import long_to_bytes
#p+q用x表示
#(p+1)(q+1)用y表示
x = 0x1232fecb92adead91613e7d9ae5e36fe6bb765317d6ed38ad890b4073539a6231a6620584cea5730b5af83a3e80cf30141282c97be4400e33307573af6b25e2ea
y = 0x5248becef1d925d45705a7302700d6a0ffe5877fddf9451a9c1181c4d82365806085fd86fbaab08b6fc66a967b2566d743c626547203b34ea3fdb1bc06dd3bb765fd8b919e3bd2cb15bc175c9498f9d9a0e216c2dde64d81255fa4c05a1ee619fc1fc505285a239e7bc655ec6605d9693078b800ee80931a7a0c84f33c851740
d = 0x2dde7fbaed477f6d62838d55b0d0964868cf6efb2c282a5f13e6008ce7317a24cb57aec49ef0d738919f47cdcd9677cd52ac2293ec5938aa198f962678b5cd0da344453f521a69b2ac03647cdd8339f4e38cec452d54e60698833d67f9315c02ddaa4c79ebaa902c605d7bda32ce970541b2d9a17d62b52df813b2fb0c5ab1a5
c = 0x50ae00623211ba6089ddfae21e204ab616f6c9d294e913550af3d66e85d0c0693ed53ed55c46d8cca1d7c2ad44839030df26b70f22a8567171a759b76fe5f07b3c5a6ec89117ed0a36c0950956b9cde880c575737f779143f921d745ac3bb0e379c05d9a3cc6bf0bea8aa91e4d5e752c7eb46b2e023edbc07d24a7c460a34a9a
n = y - x - 1
m = pow(c,d,n)
print long_to_bytes(m)
|
其实这个题也不是很难哈,就是替换一下什么的的数学小游戏罢了。真正难的在最后面。
2025.03更新:该节大部分内容都已合并到 CTF_RSA解密学习指南(一) 文章中了,故这里进行了大量删减。
待整理
1、费马小定理
2、中国剩余定理
3、







