本篇文章主要讲解在 CTF 竞赛中遇到的各种各样的 RSA 题型。
包括:低加密指数分解攻击、Roll按行加密、模不互素、共模攻击、低解密指数攻击、根据公钥计算得到私钥、分解n得到相同的几个p、已知n,e,d求p,q、私钥文件修复、低加密指数广播攻击、已知dp,dq求解m、CopperSmith定理攻击、已知e,n,dp,c求m、N分解出多个不同的因子、LSB Oracle Attack、PKCS1_OAEP模式的RSA、已知p+q和(p+1)(q+1)、已知p-q和n等。
本文中的所有题目附件及解题脚本均已上传到 github 项目,有需要的可以自行下载:
https://github.com/Mr-Aur0ra/RSA
在 RSA 中 e 也称为加密指数。由于 e 是可以随意选取的,选取小一点的 e 可以缩短加密时间(比如 e=2, e=3),但是选取不当的话,就会造成安全问题。下面就是 e 选取的太小导致存在的安全问题。
在 RSA 加密中,由于 e 只有 2,相当于把明文m平方了而已,得到的 c 也比 n 小很多。尝试把 c 开根号看能否得到明文。Python 自带的开根号求解的数并不打。我们可以使用 gmpy2 库来对大整数开根号。
题目: 01-西湖论剑rsa
1
2
3
4
|
已知:
e=2
c=9217979941366220275377875095861710925207028551771520610387238734819759256223080175603032167658086669886661302962985046348865181740591251321966682848536331583243529
求明文m?
|
解题:
1
2
3
4
5
6
7
8
9
10
|
#!/usr/bin/python
#coding:utf-8
import gmpy2
import libnum
c = 9217979941366220275377875095861710925207028551771520610387238734819759256223080175603032167658086669886661302962985046348865181740591251321966682848536331583243529
m = gmpy2.isqrt(c)
m = int(m)
m_text = libnum.n2s(m)
print(m_text)
|
Rabin加密是RSA的衍生算法,可以百度或阅读:
https://en.wikipedia.org/wiki/Rabin_cryptosystem
e=2 是 Rabin 加密典型特征,但并不是所有的 RSA 在 e=2 时都是 Rabin 加密。
Rabin 解密的 Python 实现:
1
2
3
4
5
6
7
8
9
10
11
|
def rabin_decrypt(c, p, q, e=2):
n = p * q
mp = pow(c, (p + 1) / 4, p)
mq = pow(c, (q + 1) / 4, q)
yp = gmpy2.invert(p, q)
yq = gmpy2.invert(q, p)
r = (yp * p * mq + yq * q * mp) % n
rr = n - r
s = (yp * p * mq - yq * q * mp) % n
ss = n - s
return (r, rr, s, ss)
|
题目: 02-Jarvis OJ -Crypto-Hard RSA

确实如题目描述的一般,出题人做手脚了,按照之前做 MediumRSA 的步骤做完全做不出来,而且求 d 的时候就会报错找不到 e 的模反数:
1
|
ValueError: no invmod for given @a and @n
|
所以要多积累一些题型,这里就是考察的 e=2 时,Rabin 加密中的 N 可被分解。
首先通过 openssl 提取公钥的信息:

我们得到e=2,n=0xC2636….
然后分解 n 得到 p 和 q:

然后就可以写 Python 脚本了:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
#!/usr/bin/python
#coding:utf-8
import gmpy2
import libnum
e = 2
n = 87924348264132406875276140514499937145050893665602592992418171647042491658461
p = 275127860351348928173285174381581152299
q = 319576316814478949870590164193048041239
c=int(open('./flag.enc','rb').read().encode('hex'),16)
mp=pow(c,(p+1)/4,p)
mq=pow(c,(q+1)/4,q)
yp=gmpy2.invert(p,q)
yq=gmpy2.invert(q,p)
r=(yp*p*mq+yq*q*mp)%n
rr=n-r
s=(yp*p*mq-yq*q*mp)%n
ss=n-s
print libnum.n2s(r)
print libnum.n2s(rr)
print libnum.n2s(s)
print libnum.n2s(ss)
|
记住这是模板,以后有类似的题目直接拿来用就好,对了一般读取文件获得变量 c 的值都是这样表示的,这会使代码看上去更简洁。
适用情况:e较小,一般为3。
公钥e很小,明文m也不大的话,于是 $m^e=k*n+m$ 中的的 k 值很小甚至为0,爆破 k 或直接开三次方即可。
攻击原理:假设用户使用的密钥 e=3。考虑到加密关系满足:
$$
C ≡ m^3 \ mod \ N
$$
那么:
$$
m^3 =C + k * N \
$$
$$
m = \sqrt[3]{C + k\ *\ N}\
$$
攻击者可以从小到大枚举 k,依次开三次根,直到开出整数为止。
题目: 03-Jarvis OJ-Crypto-Extremely RSA

因为 e=3,很可能存在小名文攻击,于是直接写脚本进行爆破。
解题脚本:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
#!/usr/bin/python
#coding:utf-8
import gmpy2
import binascii
import libnum
import time
from Crypto.Util.number import long_to_bytes
n=0xB0BEE5E3E9E5A7E8D00B493355C618FC8C7D7D03B82E409951C182F398DEE3104580E7BA70D383AE5311475656E8A964D380CB157F48C951ADFA65DB0B122CA40E42FA709189B719A4F0D746E2F6069BAF11CEBD650F14B93C977352FD13B1EEA6D6E1DA775502ABFF89D3A8B3615FD0DB49B88A976BC20568489284E181F6F11E270891C8EF80017BAD238E363039A458470F1749101BC29949D3A4F4038D463938851579C7525A69984F15B5667F34209B70EB261136947FA123E549DFFF00601883AFD936FE411E006E4E93D1A00B0FEA541BBFC8C5186CB6220503A94B2413110D640C77EA54BA3220FC8F4CC6CE77151E29B3E06578C478BD1BEBE04589EF9A197F6F806DB8B3ECD826CAD24F5324CCDEC6E8FEAD2C2150068602C8DCDC59402CCAC9424B790048CCDD9327068095EFA010B7F196C74BA8C37B128F9E1411751633F78B7B9E56F71F77A1B4DAAD3FC54B5E7EF935D9A72FB176759765522B4BBC02E314D5C06B64D5054B7B096C601236E6CCF45B5E611C805D335DBAB0C35D226CC208D8CE4736BA39A0354426FAE006C7FE52D5267DCFB9C3884F51FDDFDF4A9794BCFE0E1557113749E6C8EF421DBA263AFF68739CE00ED80FD0022EF92D3488F76DEB62BDEF7BEA6026F22A1D25AA2A92D124414A8021FE0C174B9803E6BB5FAD75E186A946A17280770F1243F4387446CCCEB2222A965CC30B3929
e=3
res=0 #res是m
c=int(open('flag.enc','rb').read().encode('hex'),16)
print time.asctime()
for k in xrange(200000000):
if gmpy2.iroot(c+n*k,3)[1]==1:
res=gmpy2.iroot(c+n*k,3)[0]
print k,res
print long_to_bytes(res)
print time.asctime()
break
|
我爆破了7分钟,爆破的时候别以为你电脑坏了或者这个脚本坏了哈。

自己爆破 flag 哈,flag 不给看。
顾名思义,这里的的加密是按行进行的。
题目: 04-实验吧—RSAROLL

不要总是觉得密文 C 就是一连串的字符串,密文 C 也可以是分行的,记住不要把分行符删除让 密文 C 变为一个字符串。应该按行进行解密。
n为920139713,e为19,手动把加密的部分另存为一份文件roll.txt。
解题脚本:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
#!/usr/bin/python
#coding:utf-8
import gmpy2
from Crypto.Util.number import long_to_bytes
n = 920139713
p = 49891
q = 18443
e = 19
phi = (p-1)*(q-1)
d = gmpy2.invert(e,phi)
m = ""
with open('roll.txt','r') as f:
for c in f.readlines():
m += long_to_bytes(pow(int(c), d, n))
print m
|
适用情况:存在两个或更多模数 ,且gcd(N1,N2)!=1 也就是 N1 和 N2 不互质。
多个模数 n 共用质数,则可以很容易利用欧几里得算法求得他们的质因数之一 gcd(N1,N2) ,然后这个最大公约数可用于分解模数分别得到对应的 p 和 q,即可进行解密。实现参照本文欧几里得算法 部分和 RSA 解密部分。
题目: 05-存货1
N is 18674375108313094928585156581138941368570022222190945461284402673204018075354069827186085851309806592398721628845336840532779579197302984987661547245423180760958022898546496524249201679543421158842103496452861932183144343315925106154322066796612415616342291023962127055311307613898583850177922930685155351380500587263611591893137588708003711296496548004793832636078992866149115453883484010146248683416979269684197112659302912316105354447631916609587360103908746719586185593386794532066034112164661723748874045470225129298518385683561122623859924435600673501186244422907402943929464694448652074412105888867178867357727
e is 65537
message is 0x8BD7BF995BF9E16A0D04ADB49A2411C74FFDB0DB4F35DB3A79A1B44691947C9824085BC4CA5F7F4EFA3C8FD0BC3E870AA6D5E15307A63A2172C44C5903D35785B8D06B51651EE7106B070D5A6AABA089AB67609661265B74914C865F863DC1D2DC08CE0B026107A74EC3FDC62666B50110B9D15A243EAAD6F53646929A3369285404868E42DD0BBE92D956018E3C0B36EF5E9516E433228CFDD06D6E662EC0A9A31061EA11F61CA17EABF43D2D4977FC9D6FC53AB6DC01509401B8D9A46B59A9ADAA97D54CC50C27445E4C21B893510620EC3566AD6E8727FA147437B207505217E6F2DF009E2286C8354D281374D7802D08A2062FE48DBF135BBCAB120EBF84
N is 20071978783607427283823783012022286910630968751671103864055982304683197064862908267206049336732205051588820325894943126769930029619538705149178241710069113634567118672515743206769333625177879492557703359178528342489585156713623530654319500738508146831223487732824835005697932704427046675392714922683584376449203594641540794557871881581407228096642417744611261557101573050163285919971711214856243031354845945564837109657494523902296444463748723639109612438012590084771865377795409000586992732971594598355272609789079147061852664472115395344504822644651957496307894998467309347038349470471900776050769578152203349128951
e is 65537
message is 0x8C3CF3161AA3E37831030985C60566A7604688B73E5B1D3B36E72EF06ED4F71289EFE80E0D94BD755034E6C210F17DA85B9D0388F3AD104C68BC514A8EB1569A109EB5F266F7C5FA4DDFA638258949B43D4CF1406720CCD4CA11E74FDF8AEB35C56A79781C87157FC4213573329C5B0FF411F8A4F34580AA103DB9FD403C0D409FA11860A7C4595FDC49DC2CF94E5112B772E5DEC8F17E24B10A7FD7A95DCB87BE5E27C32FC931574A7847BC506A61EFE9DB3D3F612143845FE80D7B3EA548B886A67A29CBDB2775B1F91178B6DA763F1A6ECFF46592E4C7FFAAB6C9FEF29D9CB9E035A3D98ECFFB26BA2EEAA56D1CD096E6A2CF9A58086CAD7718DDA5CB0C1B
求明文m?
这里把明文字符串一分为二做了分别做了 RSA 加密,上面的 message 其实就是密文 c。关键是加密时它们多个模数使用了相同的质数 e,而且模数 N1 和 N2 不互素,所以可以进行模不互素攻击。
判断两个数是否互素的脚本:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
#!/usr/bin/python
#coding:utf-8
def gcd(a,b): #判断来两个数是否互素,辗转相除法
if(b==0):
return a
else:
return gcd(b,a%b)
def main():
x = 17 #x,y的值根据需要修改即可
y = 65537
if gcd(x,y)==1: #如果两个数的最大公约数是1,那么两数互素。
print str(x)+" "+str(y) + "两个数互素"
else:
print str(x)+" "+str(y) + "两个数不互素"
if __name__=="__main__":
main()
|

题目是给出的文件rsa2.txt,为了方便Python直接读取文件为变量赋值,这里把无关的解释性东西删除掉,生成新的tmp.txt文件。
内容如下:

解题脚本:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
#!/usr/bin/python
#coding:utf-8
import gmpy2
from Crypto.Util.number import long_to_bytes
lines = open('tmp.txt','r').readlines()
c1 = int(lines[2],16)
c2 = int(lines[6],16)
n1 = int(lines[0])
n2 = int(lines[4])
p12 = gmpy2.gcd(n1, n2)
assert (p12 != 1)
q1 = n1 / p12
q2 = n2 / p12
e = 0x10001
d1 = gmpy2.invert(e, (p12 - 1) * (q1 - 1))
d2 = gmpy2.invert(e, (p12 - 1) * (q2 - 1))
m1 = pow(c1, d1, n1)
m2 = pow(c2, d2, n2)
print long_to_bytes(m1)+long_to_bytes(m2)
|
适用情况:明文 m、模数 n 相同,公钥指数 e、密文 c 不同,gcd(e1,e2)==1 也就是 e1 和 e2 互质。
对同一明文的多次加密使用相同的模数和不同的公钥指数可能导致共模攻击。
题目: 06-Jarvis OJ -Crypto-very hard RSA

这个题目就比较有意思了,4096位的 RSA 加密,要不是这里存在共模攻击说不定你死活都解不开。哈哈哈,要是有量子计算机的话说不定能解开。
题目给出了两个文件:flag.enc 文件以及一个 easyRSA.py 的加密脚本。
通过分析加密脚本可知,该加密脚本首先会从 flag.txt 中读取字符串 flag,然后对 flag 根据不同的 e 的值进行两次 RSA 加密,并分别将密文保存到了 flag.enc1 和 flag.enc2 中。
我们发现明文 m、模数 n 相同,但是公钥指数 e1 和 e2 不同,而且 e1 与 e2 互素(上面给过判断2数是否互素的脚本),所以这就是典型的共模攻击。


解题脚本:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
#!/usr/bin/python
#coding:utf-8
import gmpy2
from Crypto.Util.number import long_to_bytes
def egcd(a,b):
if b==0:
return a,1,0
else:
g,x,y=egcd(b,a%b)
return g,y,x-a//b*y
e1 = 17
e2 = 65537
n = n1 = n2 = 0x00b0bee5e3e9e5a7e8d00b493355c618fc8c7d7d03b82e409951c182f398dee3104580e7ba70d383ae5311475656e8a964d380cb157f48c951adfa65db0b122ca40e42fa709189b719a4f0d746e2f6069baf11cebd650f14b93c977352fd13b1eea6d6e1da775502abff89d3a8b3615fd0db49b88a976bc20568489284e181f6f11e270891c8ef80017bad238e363039a458470f1749101bc29949d3a4f4038d463938851579c7525a69984f15b5667f34209b70eb261136947fa123e549dfff00601883afd936fe411e006e4e93d1a00b0fea541bbfc8c5186cb6220503a94b2413110d640c77ea54ba3220fc8f4cc6ce77151e29b3e06578c478bd1bebe04589ef9a197f6f806db8b3ecd826cad24f5324ccdec6e8fead2c2150068602c8dcdc59402ccac9424b790048ccdd9327068095efa010b7f196c74ba8c37b128f9e1411751633f78b7b9e56f71f77a1b4daad3fc54b5e7ef935d9a72fb176759765522b4bbc02e314d5c06b64d5054b7b096c601236e6ccf45b5e611c805d335dbab0c35d226cc208d8ce4736ba39a0354426fae006c7fe52d5267dcfb9c3884f51fddfdf4a9794bcfe0e1557113749e6c8ef421dba263aff68739ce00ed80fd0022ef92d3488f76deb62bdef7bea6026f22a1d25aa2a92d124414a8021fe0c174b9803e6bb5fad75e186a946a17280770f1243f4387446ccceb2222a965cc30b3929L
c1=int(open('./flag.enc1','rb').read().encode('hex'),16)
c2=int(open('./flag.enc2','rb').read().encode('hex'),16)
assert n1==n2
# s1=gmpy2.invert(e1,e2)
s1=egcd(e1,e2)[1]
s2=egcd(e1,e2)[2]
#此处判断s1和s2是否小于0,因为pow()函数里s1和s2不能为负,
if(s1<0):
s1=-s1
c1=gmpy2.invert(c1,n)#若s1为负,s1取正,c1取逆
if(s2<0):
s2=-s2
c2=gmpy2.invert(c2,n)
m=pow(c1,s1,n) * pow(c2,s2,n) %n
print(long_to_bytes(m))
|
其中,函数 egcd 是扩展欧几里得算法的一个实现,用于找到两个整数 a 和 b 的最大公约数 (GCD),以及贝祖等式的系数 x 和 y(这些系数是满足等式 ax + by = gcd(a,b) 的整数)。
针对函数 egcd 我们这里解释一下。
1
2
3
|
def egcd(a, b):
if b == 0:
return a, 1, 0
|
在函数的第一部分,它检查 b 是否为零。如果是,那么 a 和 0 的最大公约数就是 a,并且系数分别是 1 和 0,满足等式a*1 + 0*0 = a。然后它返回这三个值。
1
2
|
else:
g, x, y = egcd(b, a % b)
|
如果 b 不是零,函数会递归调用自己,传入 b 和 a 除以 b 的余数(a % b)。这是基于这样一个性质:a 和 b 的最大公约数与 b 和 a % b 的最大公约数相同。递归调用最终会达到基本情况,即 b 为零。
1
|
return g, y, x - a // b * y
|
递归调用返回后,函数会计算满足原始输入 a 和 b 的贝祖等式的 x 和 y 的新值。具体的计算方法如下:
- g 是两个数的最大公约数,在递归中保持不变。
- y 是原来的 x 值,即在递归过程中 a % b 的系数。
- x - a // b * y 是根据贝祖等式计算出的新的 x 值,a // b 是 a 除以 b 的商,x - a // b * y 就是新的 x 值,即原来的 y 值减去 a 除以 b 的商乘以原来的 x 值。
这个算法通过不断递归,直到 b 为零时结束,最终能找到最大公约数,并且计算出满足 ax + by = gcd(a, b) 的整数 x 和 y。
上述脚本:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
#!/usr/bin/python
#coding:utf-8
import gmpy2
from Crypto.Util.number import long_to_bytes
def egcd(a,b):
if b==0:
return a,1,0
else:
g,x,y=egcd(b,a%b)
return g,y,x-a//b*y
e1 = 17
e2 = 65537
n = n1 = n2 = 0x00b0bee5e3e9e5a7e8d00b493355c618fc8c7d7d03b82e409951c182f398dee3104580e7ba70d383ae5311475656e8a964d380cb157f48c951adfa65db0b122ca40e42fa709189b719a4f0d746e2f6069baf11cebd650f14b93c977352fd13b1eea6d6e1da775502abff89d3a8b3615fd0db49b88a976bc20568489284e181f6f11e270891c8ef80017bad238e363039a458470f1749101bc29949d3a4f4038d463938851579c7525a69984f15b5667f34209b70eb261136947fa123e549dfff00601883afd936fe411e006e4e93d1a00b0fea541bbfc8c5186cb6220503a94b2413110d640c77ea54ba3220fc8f4cc6ce77151e29b3e06578c478bd1bebe04589ef9a197f6f806db8b3ecd826cad24f5324ccdec6e8fead2c2150068602c8dcdc59402ccac9424b790048ccdd9327068095efa010b7f196c74ba8c37b128f9e1411751633f78b7b9e56f71f77a1b4daad3fc54b5e7ef935d9a72fb176759765522b4bbc02e314d5c06b64d5054b7b096c601236e6ccf45b5e611c805d335dbab0c35d226cc208d8ce4736ba39a0354426fae006c7fe52d5267dcfb9c3884f51fddfdf4a9794bcfe0e1557113749e6c8ef421dba263aff68739ce00ed80fd0022ef92d3488f76deb62bdef7bea6026f22a1d25aa2a92d124414a8021fe0c174b9803e6bb5fad75e186a946a17280770f1243f4387446ccceb2222a965cc30b3929L
c1=int(open('./flag.enc1','rb').read().encode('hex'),16)
c2=int(open('./flag.enc2','rb').read().encode('hex'),16)
assert n1==n2
# s1=gmpy2.invert(e1,e2)
s1=egcd(e1,e2)[1]
s2=egcd(e1,e2)[2]
#此处判断s1和s2是否小于0,因为pow()函数里s1和s2不能为负,
if(s1<0):
s1=-s1
c1=gmpy2.invert(c1,n)#若s1为负,s1取正,c1取逆
if(s2<0):
s2=-s2
c2=gmpy2.invert(c2,n)
m=pow(c1,s1,n) * pow(c2,s2,n) %n
print(long_to_bytes(m))
|
简化版的脚本:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
#!/usr/bin/python
#coding:utf-8
import gmpy2
from Crypto.Util.number import long_to_bytes
e1 = 17
e2 = 65537
n = 0x00b0bee5e3e9e5a7e8d00b493355c618fc8c7d7d03b82e409951c182f398dee3104580e7ba70d383ae5311475656e8a964d380cb157f48c951adfa65db0b122ca40e42fa709189b719a4f0d746e2f6069baf11cebd650f14b93c977352fd13b1eea6d6e1da775502abff89d3a8b3615fd0db49b88a976bc20568489284e181f6f11e270891c8ef80017bad238e363039a458470f1749101bc29949d3a4f4038d463938851579c7525a69984f15b5667f34209b70eb261136947fa123e549dfff00601883afd936fe411e006e4e93d1a00b0fea541bbfc8c5186cb6220503a94b2413110d640c77ea54ba3220fc8f4cc6ce77151e29b3e06578c478bd1bebe04589ef9a197f6f806db8b3ecd826cad24f5324ccdec6e8fead2c2150068602c8dcdc59402ccac9424b790048ccdd9327068095efa010b7f196c74ba8c37b128f9e1411751633f78b7b9e56f71f77a1b4daad3fc54b5e7ef935d9a72fb176759765522b4bbc02e314d5c06b64d5054b7b096c601236e6ccf45b5e611c805d335dbab0c35d226cc208d8ce4736ba39a0354426fae006c7fe52d5267dcfb9c3884f51fddfdf4a9794bcfe0e1557113749e6c8ef421dba263aff68739ce00ed80fd0022ef92d3488f76deb62bdef7bea6026f22a1d25aa2a92d124414a8021fe0c174b9803e6bb5fad75e186a946a17280770f1243f4387446ccceb2222a965cc30b3929L
c1=int(open('./flag.enc1','rb').read().encode('hex'),16)
c2=int(open('./flag.enc2','rb').read().encode('hex'),16)
_, r, s = gmpy2.gcdext(e1, e2)
m = pow(c1, r, n) * pow(c2, s, n) % n
print long_to_bytes(m)
|
在 RSA 中 d 也称为解密指数,当 d 比较小的时候,e 也就显得特别大了。
适用情况:e 过大或过小(一般 e 过大时使用)
在 e 过大或过小的情况下,可使用算法从 e 中快速推断出 d 的值,进而求出 m。详细的算法原理可以阅读: RSA大礼包-Tr0y’s Blog。
题目: 07-存货2
1
2
3
4
|
n = 460657813884289609896372056585544172485318117026246263899744329237492701820627219556007788200590119136173895989001382151536006853823326382892363143604314518686388786002989248800814861248595075326277099645338694977097459168530898776007293695728101976069423971696524237755227187061418202849911479124793990722597L
e = 354611102441307572056572181827925899198345350228753730931089393275463916544456626894245415096107834465778409532373187125318554614722599301791528916212839368121066035541008808261534500586023652767712271625785204280964688004680328300124849680477105302519377370092578107827116821391826210972320377614967547827619L
c = 38230991316229399651823567590692301060044620412191737764632384680546256228451518238842965221394711848337832459443844446889468362154188214840736744657885858943810177675871991111466653158257191139605699916347308294995664530280816850482740530602254559123759121106338359220242637775919026933563326069449424391192
求明文m?
|
首先需要需要下载工具rsa-wiener-attack :
1
|
git clone https://github.com/pablocelayes/rsa-wiener-attack
|
然后把 exp.py 放入这个目录中运行即可:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
#!/usr/bin/python
#coding:utf-8
import gmpy2
from Crypto.PublicKey import RSA
import ContinuedFractions, Arithmetic
from Crypto.Util.number import long_to_bytes
def wiener_hack(e, n):
# firstly git clone https://github.com/pablocelayes/rsa-wiener-attack.git !
frac = ContinuedFractions.rational_to_contfrac(e, n)
convergents = ContinuedFractions.convergents_from_contfrac(frac)
for (k, d) in convergents:
if k != 0 and (e * d - 1) % k == 0:
phi = (e * d - 1) // k
s = n - phi + 1
discr = s * s - 4 * n
if (discr >= 0):
t = Arithmetic.is_perfect_square(discr)
if t != -1 and (s + t) % 2 == 0:
print("Hacked!")
return d
return False
def main():
n = 460657813884289609896372056585544172485318117026246263899744329237492701820627219556007788200590119136173895989001382151536006853823326382892363143604314518686388786002989248800814861248595075326277099645338694977097459168530898776007293695728101976069423971696524237755227187061418202849911479124793990722597L
e = 354611102441307572056572181827925899198345350228753730931089393275463916544456626894245415096107834465778409532373187125318554614722599301791528916212839368121066035541008808261534500586023652767712271625785204280964688004680328300124849680477105302519377370092578107827116821391826210972320377614967547827619L
c = 38230991316229399651823567590692301060044620412191737764632384680546256228451518238842965221394711848337832459443844446889468362154188214840736744657885858943810177675871991111466653158257191139605699916347308294995664530280816850482740530602254559123759121106338359220242637775919026933563326069449424391192
d = wiener_hack(e, n)
m = pow(c,d,n)
print long_to_bytes(m)
if __name__=="__main__":
main()
|

这种题型需要使用 RsaCtfTools 根据公钥生成私钥
题目: 08-存货3
题目只给出了两个文件(一个私钥文件和一个密文文件)
按照常规查看提取一下公钥文件,发现n特别大,无法直接分解为 p 和 q,而且 e 也不存在是特殊值的可能,也不存在其他的攻击方法。
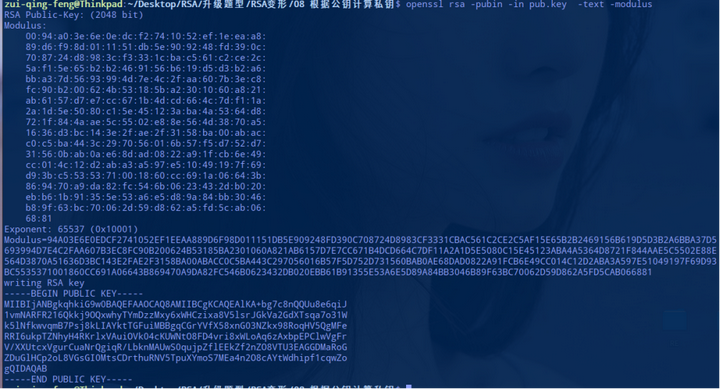
首先进入 RsaCtfTools,接着执行下面的命令生成私钥。
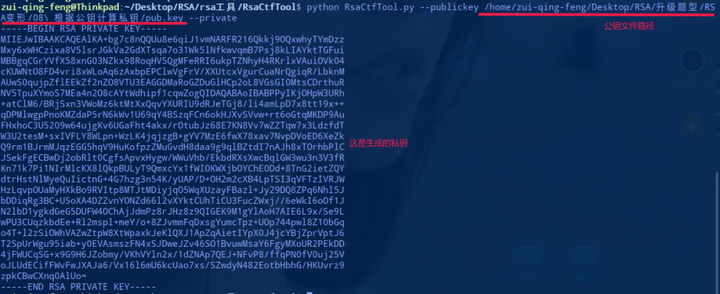
接着把这些内容复制到新创建的文件 pri.key 中。
使用 openssl 通过私钥文件进行解密:

打开生成的文件 txt 即可得到 flag。
题目: 09-存货4
题目给出两个文件,一个文件是加密脚本 encrypt.py,另一个是加密脚本输出的文件 2.txt。
下面是我注释了的加密脚本:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
import gmpy2
import random
from Crypto.Util.number import *
from flag import flag
def generate_key(1024):
p = getPrime(1024)
r = random.randint(2, 10)
s = random.randint(r, 1024)
while True:
e = random.randint(3, p**r*(p-1))
if gmpy2.gcd(e, p**s*(p-1)) == 1:
break
pubkey = (long(e), long(p**r)) #返回e和p^r
return pubkey
def crypt(msg, pubkey):
e, n = pubkey #e,n=p^r
m = bytes_to_long(msg)
assert m < n - 1
enc = pow(m, e, n)
return long_to_bytes(enc)
nbit = 1024
pubkey = generate_key(1024)
print 'pubkey =', pubkey #输出e和p^r
msg = flag值
enc = crypt(msg, pubkey)
print 'enc =\n', enc.encode('base64')
|
下面是我当时做题时解题思路:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
RSA加密:
pow(enc,e,N)
RSA解密:
n==>p,q
phi=(p-1)*(q-1)
d = gmpy2.invert(e,phi)
m=pow(enc,d,n)
本题常规解题思路:
enc已知 n已知 d?==> e已知 ,求phi ==>求p和q
看着加密脚本中多次出现p及p^r,
本打算直接开用p=gmpy2.iroot(n,r)[0] 开多次方根求p,进而求q
//根据加密脚本逆运算 未果 开不出来 ╮(╯▽╰)╭
另一种思路:
e太大 可使用算法从e中快速推断出d的值。 可使用Wiener’s Attack进行解d
求出d可直接求m
但是这样也确实解不出来
好吧 正确解题思路:
n==>分解n得到k个p 即n=p**k
phi=(p**k)-(p**k-1) //由欧拉函数得
d = gmpy2.invert(e,phi)
m=pow(enc,d,n)
|
浅谈欧拉函数 liuzibujian的博客-CSDN博客_欧拉函数。
题目中幂使用的是 r 而不是 k。
解题脚本:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
#!/usr/bin/python
#coding:utf-8
import base64
import gmpy2
import libnum
from Crypto.Util.number import long_to_bytes,bytes_to_long
c = "YXmuOsaD1W4poLAG2wPrJ/nYZCkeOh2igCYKnZA6ecCeJadT6B3ZVTciPN6LJ8AcAsRXNnkC6+9PNJPhmosSG5UGGbpIcg2JaZ1iA8Sm3fGiFacGvQsJOqqIWb01rjaQ3rDBKB331rrNo9QNOfMnjKr0ejGG+dNObTtvnskICbYbNnSxMxLQF57H5JnWZ3LbbKQ493vmZzwvC6iH8blNPAp3dBlVzDqIAmxmUbk0OzFjPoHphD1oxHdzXyQNW+sLxVldrf9xcItq92jN5sqBYrG8wADIqY1/sqhTMZvkIYFMHqoMQuiRSnVrCF2h2RtGDEayLo0evgXI/0W3YveyKCHViOnG6wypcBFm91ZWdjp3fVW/4DyxW6xu9hg/NlXyRP6pT/OyQpcyTqKRuiXJLWgFUJI/8TRgyAjBLLgSd3U0N3VM8kewXw5j+fMUTCW9/Gy4iP8m52Zabx/vEKdwdGZ0QyvgvAWGUFZ96EK0g1BM/LU9Tuu2R+VKcCSCprg283x6NfYxmU26KlQE6ZrrjLmbCOe0327uaW9aDbLxZytPYIE5ZkzhSsD9JpQBKL30dCy3UKDbcuNgB6SrDddrbIuUd0/kLxuwh6kTqNbC4NDrOT4WAuP4se8GGOK8Wz0dL6rE6FkzMnI4Qg501MTSNQZ4Bp7cNf6H9lTa/4DNOl0="
e = 58134567416061346246424950552806959952164141873988197038339318172373514096258823300468791726051378264715940131129676561677588167620420173326653609778206847514019727947838555201787320799426605222230914672691109516799571428125187628867529996213312357571123877040878478311539048041218856094075106182505973331343540958942283689866478426396304208219428741602335233702611371265705949787097256178588070830596507292566654989658768800621743910199053418976671932555647943277486556407963532026611905155927444039372549162858720397597240249353233285982136361681173207583516599418613398071006829129512801831381836656333723750840780538831405624097443916290334296178873601780814920445215584052641885068719189673672829046322594471259980936592601952663772403134088200800288081609498310963150240614179242069838645027877593821748402909503021034768609296854733774416318828225610461884703369969948788082261611019699410587591866516317251057371710851269512597271573573054094547368524415495010346641070440768673619729280827372954003276250541274122907588219152496998450489865181536173702554116251973661212376735405818115479880334020160352217975358655472929210184877839964775337545502851880977049299029101466287659419446724781305689536816523774995178046989696610897508786776845460908137698543091418571263630383061605011820139755322231913029643701770497299157169690586232187419462594477116374977216427311975598620616618808494138669546120288334682865354702356192972496556372279363023366842805886601834278434406709218165445335977049796015123909789363819484954615665668979
p = 165740755190793304655854506052794072378181046252118367693457385632818329041540419488625472007710062128632942664366383551452498541560538744582922713808611320176770401587674618121885719953831122487280978418110380597358747915420928053860076414097300832349400288770613227105348835005596365488460445438176193451867
n = p**4
phi = p**4-p**3
#c = int(base64.b64decode(c).encode('hex'),16) 延伸
c = bytes_to_long(c.decode('base64'))
d = gmpy2.invert(e,phi)
m = pow(c,d,n)
print long_to_bytes(m)
|
一看这个标题你就应该有个觉悟,n 一定无法直接分解得到 p 和 q。
题目: 10-存货5
题目给出了两个文件,一个是加密脚本 chall.py,一个是加密后输出的内容 output.txt。
分析一下加密脚本:
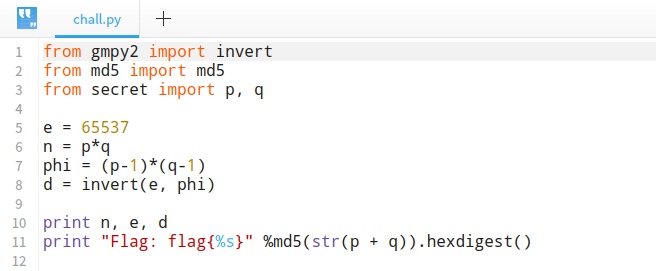
加密脚本真的是很简单啊,flag 就是 str(p+q) 进行 md5 运算之后的得到的字符串,从 output.txt 中可以得到 n, e, d。
现在的关键问题就是求出 p 和 q 来,google 一把梭好像可以找到这种骚操作,当时线上比赛做这个题目的时候真的就是 google 找到的类似题目,百度啊,可不可以靠谱一点。
解题脚本:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
#!/usr/bin/python
#coding:utf-8
import random
from md5 import md5
def gcd(a, b):
if a < b:
a, b = b, a
while b != 0:
temp = a % b
a = b
b = temp
return a
def getpq(n,e,d):
p = 1
q = 1
while p==1 and q==1:
k = d * e - 1
g = random.randint ( 0 , n )
while p==1 and q==1 and k % 2 == 0:
k /= 2
y = pow(g,k,n)
if y!=1 and gcd(y-1,n)>1:
p = gcd(y-1,n)
q = n/p
return p,q
def main():
n = 16352578963372306131642407541567045533766691177138375676491913897592458965544068296813122740126583082006556217616296009516413202833698268845634497478988128850373221853516973259086845725813424850548682503827191121548693288763243619033224322698075987667531863213468223654181658012754897588147027437229269098246969811226129883327598021859724836993626315476699384610680857047403431430525708390695622848315322636785398223207468754197643541958599210127261345770914514670199047435085714403641469016212958361993969304545214061560160267760786482163373784437641808292654489343487613446165542988382687729593384887516272690654309
e = 65537
d = 9459928379973667430138068528059438139092368625339079253289560577985304435062213121398231875832264894458314629575455553485752685643743266654630829957442008775259776311585654014858165341757547284112061885158006881475740553532826576260839430343960738520822367975528644329172668877696208741007648370045520535298040161675407779239300466681615493892692265542290255408673533853011662134953869432632554008235340864803377610352438146264524770710345273439724107080190182918285547426166561803716644089414078389475072103315432638197578186106576626728869020366214077455194554930725576023274922741115941214789600089166754476449453
p,q = getpq(n,e,d)
print p
print q
print "Flag: flag{%s}" %md5(str(p + q)).hexdigest()
if __name__ == '__main__':
main()
|
题目: 11-Jarvis OJ-Crypto-God Like RSA

呵呵,这个题我认了,别的不会的题目起码都能看个大概,这个题绝了,只是知道解题脚本中对应的变量是谁了(哈哈哈),顺带把变量给你们注释了,反正我是写不出来。
这里面涉及到的东西太多了,我觉得绝不单单是 Python 脚本的问题,什么数学、什么算法的,必须给你安排的明明白白的。So,我把这题作为了一个模板,以后有类似的题目,直接掏出来用,莫非这真是"上帝之手"?
题目给出三个文件,一个是公钥文件 pubkey.pem,一个是残损的私钥文件 private.corrupted,还有一个是密文文件 flag.enc。
首先使用openssl提取公钥信息:
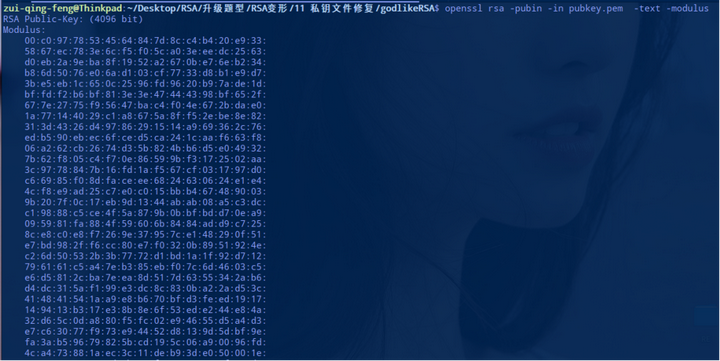
然后将提取到的公钥信息填充到恢复私钥的脚本fix.py中,然后运行这个脚本。
https://github.com/Mr-Aur0ra/RSA/blob/master/(9)%E7%A7%81%E9%92%A5%E6%96%87%E4%BB%B6%E4%BF%AE%E5%A4%8D/godlikeRSA/fix.py


接着,将私钥文件修复脚本 fix.py 恢复出私钥来,存放到文件 private.pem 中。
这就结束了吗,没有,god 不是白叫的。你会发现你根据私钥使用 openssl 直接解密密文文件解不开,而且直接根据p,q,d,c也无法直接求出 m。这里又涉及到了 RSA 加密的填充模式。
这里使用的是 PKCS1_OAEP 填充模式,参考链接。
然后,接着运行下面的脚本即可得到 flag。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
#!/usr/bin/python
# coding=utf-8
from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP
with open('pubkey.pem', 'r') as f:
key = RSA.importKey(f)
N = key.n
e = key.e
print N
print e
with open('private.pem', 'r') as f:
private = RSA.importKey(f)
oaep = PKCS1_OAEP.new(private)
with open('flag.enc', 'r') as f:
print oaep.decrypt(f.read())
|

刚才说无法根据私钥使用openssl解密密文文件,那是因为没有指定填充模式,openssl也可以指定模式。
首先,把生成的私钥保存为名为"private.pem"的私钥文件,接着执行命令进行解密。

如果选取的加密指数较低,并且使用了相同的加密指数给一个接受者的群发送相同的信息,那么可以进行广播攻击得到明文。
适用范围:模数n、密文c 不同,明文m、加密指数e 相同。一般情况下,e=k (k是题目给出的n和c的组数)。
例如:下面的就是 e=k=3
$$
\begin{aligned}
C_1 ≡ m^e \ mod \ n_1 \\
C_2 ≡ m^e \ mod \ n_2 \\
C_3 ≡ m^e \ mod \ n_3
\end{aligned}
$$
使用不同的模数 n,相同的公钥指数 e 加密相同的信息。就会得到多个 $m^e ≡ C_i \ mod \ n_i$ ,将 $m^e$ 视为一个整体 M,这就是典型的中国剩余定理适用情况。
按照本文的中国剩余定理小节容易求得 $m^e$ 的值,当 e 较小时直接开 e 方即可,可使用gmpy2.iroot(M,e)方法。
题目: 12-Jarvis OJ-2018强网杯nextrsa-Level9
题目给出n1,n2,n3,c1,c2,c3,e。求明文m的值。

解题脚本1:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
#!/usr/bin/python
#coding:utf-8
import random
from gmpy2 import invert, iroot
def broadcast(n1, n2 ,n3, c1, c2, c3):
n = [n1, n2, n3]
C = [c1, c2, c3]
N = 1
for i in n:
N *= i
Ni = []
for i in n:
Ni.append(N / i)
T = []
for i in xrange(3):
T.append(long(invert(Ni[i], n[i])))
X = 0
for i in xrange(3):
X += C[i] * Ni[i] * T[i]
m3 = X % N
m = iroot(m3, 3)
return m[0]
def main():
e = 3
c1 = 0x9e84763bdbe246fad0a9cd52fda6233e6128a6210efaf3e6dea4fe272f78ad1f8f5cc7022f62f4f542341128e42d6fd10e67c5f96edbd243917c0151289f7228e44019b8c65a541d7306b398465e26b69cab36cc61e4ac094832b4299bbaf4630b722a0fb4f1997053be97e926f94afb55a0bb6ef00ab694e2f595d9eb8ca96c49f5cbbe194529f68a1aaf6f5151484b471285ba8fc8cd30b55612f35a74dc68e255c363579a80d27ce5090873ac719ba59f2492c91fd28bcce26b6a02bae005cbbd2a4cfe5b93442be8664d2313d412e7e09f545c64b7b74bbc408b6e574d0d300135cba8d6c1d73737d59baca9992ede644d856eb4cfcda562a75743e4b491
c2 = 0x9817fdc7b31a8f9cde1794096d3aa2bc6fe06fe34d4b7c9ca9a77982adf67fd4a7e636659553f4168a16757dc3a75e54ff850b9a94a5270f4f75502c7055a3a389df2ea6b00784a4e78e66901b427253c0f343f127e0ff162a349bb14eb4c1453fc6daace19bba4940d77c435686ef3b59f732072cde2e148d1a64f9682b3f1ceb9a000d87e180a1f9eb20c59dbebc13ddb2e07b64db89217f40369aeec878a45d99909ab2a3e4cdb74aa68890c941315ae289d6667200c53f9a32c8a64bfc74e62898ac03c460f945a13f11ee28860a3cd07526c30aa92eb89442a76549fe4ed8a43d14fdeeb350e90443a3a586db719f8610eb5d4a8f5bd1e481b5ef6e96ef
c3 = 0xb0c5ee1ac47c671c918726287e70239147a0357a9638851244785d552f307ed6a049398d3e6f8ed373b3696cfbd0bce1ba88d152f48d4cea82cd5dafd50b9843e3fa2155ec7dd4c996edde630987806202e45821ad6622935393cd996968fc5e251aa3539ed593fe893b15d21ecbe6893eba7fe77b9be935ca0aeaf2ec53df7c7086349eb12792aefb7d34c31c18f3cd7fb68e8a432652ef76096096e1a5d7ace90a282facf2d2760e6b5d98f0c70b23a6db654d10085be9dcc670625646a153b52c6c710efe8eb876289870bdd69cb7b45813e4fcfce815d191838926e9d60dd58be73565cff0e10f4e80122e077a5ee720caedc1617bf6a0bb072bbd2dab0
n1 = 0x43d819a4caf16806e1c540fd7c0e51a96a6dfdbe68735a5fd99a468825e5ee55c4087106f7d1f91e10d50df1f2082f0f32bb82f398134b0b8758353bdabc5ba2817f4e6e0786e176686b2e75a7c47d073f346d6adb2684a9d28b658dddc75b3c5d10a22a3e85c6c12549d0ce7577e79a068405d3904f3f6b9cc408c4cd8595bf67fe672474e0b94dc99072caaa4f866fc6c3feddc74f10d6a0fb31864f52adef71649684f1a72c910ec5ca7909cc10aef85d43a57ec91f096a2d4794299e967fcd5add6e9cfb5baf7751387e24b93dbc1f37315ce573dc063ecddd4ae6fb9127307cfc80a037e7ff5c40a5f7590c8b2f5bd06dd392fbc51e5d059cffbcb85555L
n2 = 0x60d175fdb0a96eca160fb0cbf8bad1a14dd680d353a7b3bc77e620437da70fd9153f7609efde652b825c4ae7f25decf14a3c8240ea8c5892003f1430cc88b0ded9dae12ebffc6b23632ac530ac4ae23fbffb7cfe431ff3d802f5a54ab76257a86aeec1cf47d482fec970fc27c5b376fbf2cf993270bba9b78174395de3346d4e221d1eafdb8eecc8edb953d1ccaa5fc250aed83b3a458f9e9d947c4b01a6e72ce4fee37e77faaf5597d780ad5f0a7623edb08ce76264f72c3ff17afc932f5812b10692bcc941a18b6f3904ca31d038baf3fc1968d1cc0588a656d0c53cd5c89cedba8a5230956af2170554d27f524c2027adce84fd4d0e018dc88ca4d5d26867L
n3 = 0x280f992dd63fcabdcb739f52c5ed1887e720cbfe73153adf5405819396b28cb54423d196600cce76c8554cd963281fc4b153e3b257e96d091e5d99567dd1fa9ace52511ace4da407f5269e71b1b13822316d751e788dc935d63916075530d7fb89cbec9b02c01aef19c39b4ecaa1f7fe2faf990aa938eb89730eda30558e669da5459ed96f1463a983443187359c07fba8e97024452087b410c9ac1e39ed1c74f380fd29ebdd28618d60c36e6973fc87c066cae05e9e270b5ac25ea5ca0bac5948de0263d8cc89d91c4b574202e71811d0ddf1ed23c1bc35f3a042aac6a0bdf32d37dede3536f70c257aafb4cfbe3370cd7b4187c023c35671de3888a1ed1303L
m = broadcast(n1, n2 ,n3, c1, c2, c3)
print m
if __name__=="__main__":
main()
|
解题脚本2:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
#!/usr/bin/python
#coding:utf-8
import gmpy2
import time
def CRT(items):
N = reduce(lambda x, y: x * y, (i[1] for i in items))
result = 0
for a, n in items:
m = N / n
d, r, s = gmpy2.gcdext(n, m)
if d != 1: raise Exception("Input not pairwise co-prime")
result += a * s * m
return result % N, N
# 读入 e, n, c
e = 3
n = [8564529398597496052509875513481234511905571293608253591774352345237876733293108831203723008958367224489489969614656703455962549261315442327443089652074571708651505447379309166100331065440172781968875497386410667715026180057913363208450111095566219238303387888025161407043477291378931412269049849744457547932264137377411127192940332805452317547219248055802197050456726624516860024108642571703812719370387292166670300197241575461417648592309869669813374010765766544607691011957968652581504886331252936146901456910589102484807039294566703917033093028140452849747910537865958098720693569821256189593894121111357731919189L,12222166297277342805260668042066733749258843622057497574551492680820573970618063356710810891221670366396148862070530068431772630271300064517141331380959413811482890080103511756363920299387620181525172247384085449944650678616398890947062703879307721506228672839270493453501648644787019360131991056158375296484870723717496184332078521221915234959627683952251865227849249752415242124235776428944052873501045127442031423538183282845800971359590735184850648986263721823804859410866927117413289461014754456802566932965710529063515405296476007642849800772934170961993925017146017197762805148533435040675962332469643915192423L,5057224034499776793532654516178914954537547410664409403680432108569079856741764362023185604595829263918927121465578691201904227912897025244771553860102714429349163283510695391193774853323951653123109509215361937850724934183826508070404239791710229214063382081391564954935544392514769166830815475459218792639383796711824752291158895292103354274632470559179266550681095452239666165213986993496109747058314685303485222302144835490056402939133225003233112131275635419321982899965440912525225759368684717157077161771778903529280898069381899400305195745292409238361901176051346615633641550303346790420492393767770845418243L]
c = [20010971557789931948130798983030201950038450269144104532821030667924400788869920238579729514672630221804096063149106742412869966814701225466606392171030411339119559280790040322081104363393453503417465768386174002015870794567148694722215873094298859132439253412531445187990845476275251348800166731481176155530755581153710085966976765505591809596417849783597055650440598035159288091495453205698044687869932756053447012994409598155552263807571713982758132066319612777306466708222135510918174055647735727504029507503430288609410745159037684948343055275573269067165460711584845480188706531450367147105629493736100726092945L,19200052919818196558567528701224082155105852846109782021681848107226495293687021416871117444987923837810238872836818190457667509409714021669160815809413653880491792640346474248859559867743715715552372738909255050196638006472279364316678941257894898953088366861786500472095752890593521428325838148184891778283229870316694059734109045397448347320487605412988229047015174998893589731503114337273121463601984792339337970193596813660178636222764332155999993506914518600565394196792457144962180040786607335687020278442899146954126853580244264273526509238060494624980807993322975135366653181977147866567146492356137019414255L,1394721540127922627584993749596603212491913755865039994631041458882716953251760080638497574652888386411767951258467542002582418260315909190241131591474627765734174146981015346732559115044918706641616288474447294129332475081232268241201488455865700933615291016346552048997127415783072860387265063527874160016186183078384940312292521628077750464413013768765371508493304331719166196330883242895556903378707199640686499970367957552543041110199009425369612644492288765891769004579050802446992426813215932250347386859783813875543314196764160792696291742850356532493945652482643696238487389412404616537620013009141601852080L]
data = zip(c, n)
x, n = CRT(data)
m = gmpy2.iroot(gmpy2.mpz(x), e)[0].digits()
print m
|
解题脚本2使用的是中国剩余定理解的题,代码确实简洁。
题目: 存货6
怕你觉得上面解出来的 m 是纯数字看着不舒服,特意给你找了个带 flag 的题型,还有就是这个 e=9 也不大呀。
题目给出n1,n2,n3,c1,c2,c3,e。求明文 m 的值。

解题脚本:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
#!/usr/bin/python
#coding:utf-8
import gmpy2
import time
from Crypto.Util.number import long_to_bytes
def CRT(items):
N = reduce(lambda x, y: x * y, (i[1] for i in items))
result = 0
for a, n in items:
m = N / n
d, r, s = gmpy2.gcdext(n, m)
if d != 1: raise Exception("Input not pairwise co-prime")
result += a * s * m
return result % N, N
# 读入 e, n, c
e = 9
n = [142782424368849674771976671955176187834932417027468006479038058385550042422280158726561712259205616626939123504489410624745195777853423961104590708231562726165590769610040722589287393102301338152085670464005026301781192671834390892019478189768725018303217559795377795540494239283891894830166363576205812991157L, 153610425077816156109768509904751446801233412970601397035720458311275245730833227428213917577405780162151444202393431444812010569489900435979730559895340377469612234558042643742219128033827948585534761030527275423811282367831985007507137144308704413007806012914286105842311420933479771294576841956749281552971L, 152540067782701001222493009941492423063369171831039847414320547494725020441901272486665728360741395415762864872737675660423920609681185809510355937534756399208661762715484879562585724584849261266873624875852300611683382543315580370484972470694466195837255994159609193239840228218925381488410059939975556977947L, 125842716702134814646356078531900645012495638692517778270527426844383063904041812273637776798591687732598509470005151551320457132061693618473039437320011446697406190781306264437609046721508738109650829547010385875425097336266103994639126319889016342284747700714199556143378526590058467791687837422897022829661L, 116144389285266462769913139639175922392318396923181100785008570884082681963637784423143843845816350379438789947802939701820129805341796427821894273985551331666719808355412080909245720551238149511778060242720419584504473490216670437024863860559347959698828131475160058721701582089480924088773887932997353631767L, 127833907448946785858374094953899556339175475846831397383049660262333005992005484987913355932559627279178940862787593749842796469355336182379062826441222705075178971785791223706944120681105575965622931327112817747065200324610697178273898956820957640413744954233327851461318200323486469677469950386824833536523L, 130561613227079478921314550968562766645507834694262831586725464124109153306162445639759476845681271537955934718244296904503168256991962908095007040044300188572466395275317838178325500238288302672390013747102961340256309124310478931896245221622317302428447389760864327859640573452084295225059466376349115703119L, 115953389401040751013569404909249958538962411171147823610874077094621794755967854844224923689925397631692572916641171075740839099217316101334941033937183815345038898177087515909675028366437302462022970987947264115373697445950951595479758872029099661065186221250394358255523574834723958546450323357472451930993L, 143437107845384843564651522639125300763388830136500260725097766445883003928355325003575359566631064630487365774344508496878731109174874449170057678821440711511966073934025028100604234445470976333825866939923998344367645612128590820812489407412175198698290167077116185959180877334222693344630253253476594907313L]
c = [85033868418784308573673709960700777350314426427677627319697346811123742342359072170220428874952996988431950989321281905284522596263957356289624365171732095210045916218066135140320107686084053271623461104022705353814233772164502775939590711842361956121603943483040254727995655776263673058788416722141673409688L, 66065963470666895005407449599703926269325406456711861190876894466341571726360462706664546294453572319565476664348345756905411939632955966517708138047546806602828064213238537646393524578984547577761559965654539771172357089802682793169968961304179886652390277814477825753096636750388350662980872556701402397564L, 116011740820520887443111656288411611070614127688662643257265381793048354928820176624229624692124188995846076431510548507016903260774215950803926107831505634778278712070141663189086436127990584944132764896694777031370995058271038329228336417590284517922855284619653301817355115583540545182119702335431334401666L, 97640420284096094887471273365295984332267897927392169402918423863919914002451127544715668846623138003564829254309568918651163254043205129883843425179687841236818720463784828905460885026290909768599562386370732119591181513319548915478512030197629196018254041500662654260834562708620760373487652389789200792120L, 8112507653841374573057048967617108909055624101437903775740427861003476480616929517639719198652146909660899632120639789106782550275648578142883715280547602249589837441805676364041484345030575130408744621981440093280624046635769338568542048839419939250444929802135605724150484414516536378791500915047844188300L, 36792148360808115566234645242678223867680969786675055638670907933041180936164293809961667801099516457636164692292891528415720085345494773373966277807505798679784807614784581861287048096977968620964436947452527540958289441390882589051225367658014709290392321808926567572528170531844664734909469690750971883323L, 53043093283305492238903255767698153246673671181809989362223466090875767705978690531154079519999671834688647277179370374802495005937892824566602423646978168777735383632928274082669949750078161820002768640908750005814934158829006019656592134357897586040866207754535586785064545866404380204728594863102313407789L, 88499407133762624445946519155722583633934260410706930537441122463087556094734626189377091740335667052378955691250910459790202385799502439716173363179773811920751410726795431402796346647688144853156900427797933862087074385441977254140336390678022955770879265490567987868532251217565094093318626424653599450992L, 138337520305048557335599940473834485492131424901034295018189264168040969172072024612859307499682986987325414798210700710891033749119834960687318156171051379643844580970963540418974136891389303624057726575516576726845229494107327508855516437230240365759885913142671816868762838801720492804671259709458388192984L]
data = zip(c, n)
x, n = CRT(data)
m = gmpy2.iroot(gmpy2.mpz(x), e)[0].digits()
print long_to_bytes(m)
|

题目: 存货6-1(新增)
题目给出n1,n2,n3,c1,c2,c3求明文 m 的值。注意这次没有给出 e 的值。
1
2
3
4
5
6
|
n1=0x7d9ec519935fecf80eef98e1e500d1da3f7bdfd5b94375243c9e8cba36bf4cbd5a3cacd9d981e3710172deaf9158628b13e28eafc835bad12123ce0abd66540836e6267b50294ee8bfb7dbaf7ec5c7d593303a3329be749f6bd8226af47ddd0fe2475c4ad0560156e1efa1f91496fa279d18e12ad10bea5f72f18bcf851c22d9a9bac8f70b5a0f227dfa49019d26f673470cd1de0d0bbe0df8c57ca90b1c271733e21bd9cd28f3ae2e7fa25eacf98201fec6fdd585ae58db16f543f31cef0db2ae71e3f184a96d662604bed370ca8daede9dbdfdb39e682bc72d37c31c7d64a4e41710c8ff170075d0e7f8ec9d5a122cad33a11876e7c3def7edf6bd16b1b24aff3d677cdb421e1cd9ade2e137034ae0541631139d55d1641f5f56614feec17221aafe9aefcacd0856f8d114813e73a6e70330d4e2bba5eef984bc824fbcd987993438cc7b6da58c090be809c5b378f40459388c32756770982d0964ae9914a81a43596f306e4cae443c5eecbff4e4af521bdf20dc0c78441030eadc21257c9c7daca9de65f84678566b217e8ea0e1bffb3cd86d9056eb0a814ac4bcf23ddc51a134484d3491689f64611e83a3b35e54811a53ad8f391363f9799d5772f82bcc73ddc30939b3de2a374fa1c451ee64fa50c9a00e9dc8ed6cc787f97918908089853405c80808321202162b32edeb0935c4a1c3b15d6e7190440f445dfa1be269L
n2=0x6b794f7168ab67262328f0f90618e274c8a3f8ba2bac2c1bd2147d894150e1a29a7e92ef4193df5c95331106ac09ce65e90b6e90fc2ce13bf040a92425a97bd0661e5d8b5c5243f4ebc519d7179d05bcccb8e9746ed1281cf3e7782322dd092c515cf1ecbfb4e1f338e3f11760a0011cd102a2b1aedda70ff126ce922b4bd93a84ea09c4ec9785db18be8db02cd2885fc6e3b87e4993bfcc4973cd77ce7fbbe139b0c730138550c7fa363c0807daeb8cac020ce8acbc20a8786ff4b5bccd2a3479fa714096cdd48b29d7f8a522c1aa175b1c39c5de2dec099f9fcb2e2b1ba36f34c5b5cece9cb37e3ac5659373c15ecbc59ba5a89c90f9d19b81b99b3642d6b58d4d3a639239a9c817b4cd714eefd825caa75d083ee2aa19a20842d5b0aa71f9a95c7f5bd35d0df1a3e300a90c92183735e679e5c1be2b96d45dcf22965b914370efc890620f6633bbf4489249071c0f254b641a161c51d4f84c84b5be3eb514ab4bb52d2a2c37a66d9a6370beff5286dbaae080f809a2681d6826fc80399c4332313cab8f9a9e4553bf2f2d2ea09f4c47c472177b1c3bff4c2e4b8b30c88041e6ea6863cb5edc2215470f8ccba6a528004cf094d5a07d9b99b4730358e09cacec353a94fafad6aafef22e8f55952fba96d0d7f63cffcf672ea7550619b140dd500ec1b419a99704c91430afcc2f6f208a0e5544eab606d4884f2c96c17dc609L
n3=0xa023e410eebf1ab19c0022e5fbebbcd40787bbc886980bcbc777f25a0c9bc951da654268d5136b0cc957093d62bfd90086d4545fe02ba4a51707e5231831fc0d60070b5eccb992b321d021dea8d12118937ae7a4f2ad068ed7764fe7ae5057552308df4c64899dff6047e4ef3a74c21403f5783b19ccf6b5bdfa66ded2ada5a8708ab9edd14db3120de55fe94710834dd9015082b2269688b09d22b4d54f5a6f7606bcf07a9c2693bb96914b5faca5cf6e2964ff920f8565ecbf4d7d2458c19908607accdf881023153cfb27fa054bc6b0877e31c88fa1017d2354e58477fe8e68bc1b7a52d61150e3e447d8eaef0bcc0f0b9443b38e334bd2c2cf0546ef14c201be99097ae3a4aa4ba8d519fd77d51a3ebeb944b096cb0665dd3ccbf15a6ff0ea3faeb9163df708ad8b95e5862afb5137d0b945fca589590affd406f24888a2c86f5d4fa148573a7b7cafb9262b06b41cffeef2282782efa131b7f504e064f1904a6c7fbbf97149250719649b139550d6eb1853ac4564dffc76f807de3f0b0a8b0b58b4dc6edf1397efccc9ae08a2cae403269f0c683d3b5559c3eae03d0a910dcc9ce12ddbdca396d4c8c946ced50cbcc33d639f6d788bc98257bb6f97655f6d03cf721aa5b6d2964bfd141cdcd1b8087e04a701c156a754c659c0a19393790cd8dd05739eb6e87c23d90679538f819ab1190a381be8d20cc524d67c40cf89L
c1=0x61ce20185c2f3bb10cd0af2aa5ea62cfc7213896e15a511f6516518c6a8a644a823bb45fcd97ec6297aef54cc8a1ecf5cd7f37b75359b0052b127b4373dba37b7afae4f5a872665e0cadfcff62deba6895a0ae160da052f6fef96a1a87f2e8b9643ee54381f97cf81c38785d81e714427f1e2dd882e0403955605a44a9b85e2d8e94663c95735987fde7c60cbd3e8bd2a485bd2c32776fb2d8541709478d94a4173d5056c0b6c8a4e41465be92a317cebad1dba92b12f22df081039d08025372155bffeaea59a9a6a8a96818f7b47d7fac53dea14b763fc1983ac84e67f54c2d17fcbbd64626036e7c237e460888121af71a355da7641e4d93579c405b3778951a87d7716b9ee348e44ebb7bcc82ac75191ebae109cb885e84858bc0edfd8064e2a4cd7baa4b8d1636b404aaf2a86f555152c133e06439dc125f3dcaaff33cd5ac2a0923192b5843a8fde1bf3198ba87978fd54e2f429c93bfbd9e58372db49aaa558304b322e85c1dc64c608a9fb902956921e1bb3cc0f7ded7cd469a263d9c60950d1e132199b07f4143d47d63234ff4b24b84b866b19e3070591fdd420efe245f24aef5f43c6269cfa4ea7bc40595124f91869b0236a3de679bcfc945019a7385383d18ab1ce1e585371af20ebe6f028361c6c398811aace99f2d1cf402c89190bffb34dd388f8b926a8b8b0f146d4e1612561fad83206b94a71894da4da4L
c2=0x18ec6c682f53a49b6974a96dbb1ac33c6d55011e28acf6cc27adb1dca8db33620ed9cee7b720fe2475eb0ab7ba2ea2b7648794e1c06a0732e2737978ccafabc219259b984065caad51abe73e8fbc20889b5ac64dc75b6adea46122ba589b6c13838b154c2f78ef5782f2a284a51efa0724bc94a4d2c8fd1dadf0d3b23ef21c6144784375b808e3a3eb32059d99a3c359db6e38608196909c2fbc1211aad8fc6215aea1ad422c75dd7842b30c802849ff077a4661dc315c735591bf3e4c4004ed3f8098d4d0afa51192814a0bac7450b9f12a40b218b263c022d2868cce270510023904e0301a8f0c0cd1501c64e1cbd84905b5e801b880067468d7b68e9270b29d0b5657b6d7605ffbbbba7d5e54ac183b45cf72429ee80f98a9f2a4ef6284a4548c00e7b145b998bcdb35d73d1d61e0fc1378554eef7264ce5fc249c5a685d4905d5c9251108013ea5e62f1ee1742699bc991543624640927c1248f55f342f57746b3783659a8a0078c5b8fe14304238d02dc675416fbec6d973418979482cbeba08b81d23f49fee7abeb67bf54ed1726fe4375625225bdb2e73d4b8be5f8d50bf2c7160cd5ec93fa84cf70d28fa848a5df72c41d778b5ba02abc3845a080299527a151ef73d4ecd9f803b6d358f8b3543becf6ad50b3d968c2f3351afa97e7e8e04aa7f73a81a63ecb78856f34bcaf8f7d5c9d025a9a30352de51c74cfebc1L
c3=0x9fc32050f50e191c99070816ddb3dccd0974bf0197c1c1cd067218b5e9c0c8aac90c40245f6e2dff17bf13387bc3bc5ce9eec7bda955feac0b20ef3035a4f847ee2e207cf35002bf33c408f861eb960ed7180ee743b62e84594c237b9e7828225b69b26864ba2127fb208e57d8d16ba49ff2c5c9d294da545290ce8e007392010d6cf1c4b959786341f5d1f044ae6ff36b146d11eba9387e70ac876516d7f96fc5769cb93d46daf91b5d241ac619e3a13b4c6d6b8684cf80690838efa05e751388f3ea255672c181dd8bdcc637552e49ec7e07074b11c52ddfa9eacc4e6db0ed34bf2cbca2621bf32238cea1eb834989858bfb82554cabc60e347ce859a652e7b5eb4e37203324804a3dd66b6aed3a6a1137257fb89bf59d97a7c5fa02440b2f88bd7a4b7986e8ae4e421610adc98ece4b3ab0b66582a1d11527d60196da5c4b63cff7a875adae448e886aa5af4a27d3aac2625914c696da18fae2886710fbf23031327c94a041609da2f8588e0f72ed5355d286906a8e8f28c693e44d53e8382da6d64e9f3237ea71b06b210f3ec1cdf40c383540214dc65d1c3acfb6918c25997a4ae19397dfbc54c56bd4f26cd07187733ed91d1203bd5abadf1667e572d3fef9cc0d3ecea8fc6a3804cd9012aa4f89a1ac3613704b6f2dd566e6d6b4ae797365ca69f966158dc0d62e767bbdabc5fad52d868cec33bec3e2623e3f72d300L
|
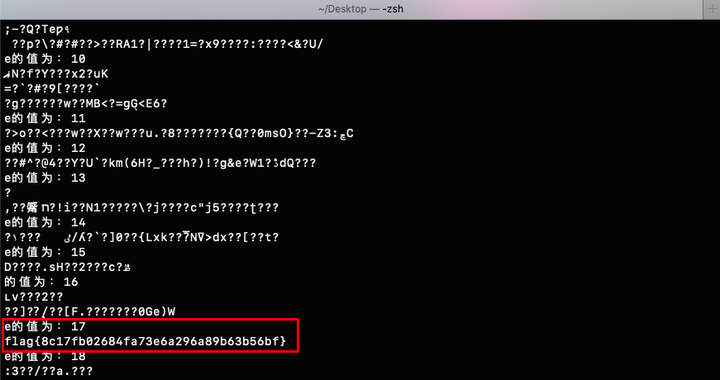
解题的话,可以先尝试 e=3,但是没解出 flag。
此时就需要爆破 e 的值,理论上讲,e 的值不可能特别大。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
#!/usr/bin/python
#coding:utf-8
import gmpy2
import time
from Crypto.Util.number import long_to_bytes
def CRT(items):
N = reduce(lambda x, y: x * y, (i[1] for i in items))
result = 0
for a, n in items:
m = N / n
d, r, s = gmpy2.gcdext(n, m)
if d != 1: raise Exception("Input not pairwise co-prime")
result += a * s * m
return result % N, N
# 读入 e, n, c
# e可以随意取大点的值,本题e很小就可以得到flag
# 所以就做了[1,100)之间的循环,你也可以取[1,65537)
# 注意e不可以为0
for e in range(1,100):
print "e的值为:"+ str(e)
n = [512485683379248627994222054928198152386318092644738180381554991475217377796405434854335056277622930547863024818767444598344410114539577997600760963632431418175495524212085227342236317690282303579871792604136978688849603906940046044534323144974053231416767418730793910263975433053461456721073431678088001273173284389468140530700307609776388997865772839512574327150259671379170026613490736333987026453811040095250243133527257805577313715212812958664333627735599163789040400505627822241159031720604542905728505522971011717666817345682281260608494735673864681250466412331593958894961131488445737536608944832487664399026112772867107087511943463538583457683579491879673641747689921593966314187930608676512863996255918764250565309330970516261788076369420228272626436321005067854817412234934831868982242339922158712560874614372107706079567173989259456857608363761805364620698478353230772690734471510134342068390134954906482464260622773680007027270240927217704723404590378763918240935998163799908756686555902792898116295063931404222813003278812035337906714468974195245694839181751219111401835806870499348487733491946647101567421316709805465910092315582508830042739317183125257526385847182925549204858279744905286118241383712008804714524959337L,438455129905663326510217996453387937818265147158140912081178396743766705601124940665790932344481155400002301338515524231925714648114810219744906401692738457749458278151114387635536422652494466839733126044697474681703619367177810933835403243322075569780826658879869369073520408208881042059373788457691248620041363036256053901332732025192473513880966852569324181325637113811528881626784815652329195878816996045400785780863488097039442217416113657576307367610903230358079374901165790819244990843302685212147937153498655927622235924092330572523305629875231791404715651959183795358420179448279473775095313467638399477146757229070378632818776284346057352441718601252186467300865188809011881157659965626389442897514625454445586427853274594179142076630186758618951856854369899214565996874415367745532324528369058533990486031307221691495860169756892482038169396339092890711719474815240465100920233523155578622866773601776749758630566368939795717596554340628161945827353855540096690670439478394005656412231410467731001387527736194221724672706430756234754940822630104576940365000003870106656376805817265622018226286424874849207544941467791006032204338343828474870841718078157179104550873232976483975616382329979719134670083763882419066043745801L,653315011935722683633899239971517941619349225695222088452194012082260326313201677835660945384275485145096065789222102748796071121711741203243670414338927148826702659529852592126552866279897276172924949211665542075745606262930965969289469269385301071552633342358778736510473222632405762525274716680890233538863243345692088160380126514797731426532170556602864402270537622591136334016473986479380886333915960074299602274671326676436465721122648878937456119562883070126768308182048342065999178801029549307888585963509968312202636585782857004099050511100978623830631609264692400949699741726049139455818499378351117228903547409337889830316549423121620369033893579169220786264356102811922557390482838303383978852873130668081323828348612838822334030273451283626768826170742066900163715681536233509267601661429117260438377187730730034557272078251624627747748768164927882629463582925338671073691854448141606348848569385399779605558939845122283956988301029392645516848789335435999529269974727866199089608234196347034929836500632922152689344010813924445789115346540480520677473336451000106471051448922245859528982264117288034012176740729039917085047680314285043383807860886975328022081757231586996665711685759320301324337611554984459865268735881L]
c = [399010311121182943332309121114907411971005715655147896283369909476319473320142906797174433944197736682155228613837419252518602898442959789436466058872795204684719139465569382123104599556182756881512146887835901762524124952169928552088784468883025949156497960737022461897943895387142452146896439885966442758514883551398180828108448038344602784548819521285900170439253491829051725879130937677485144773782521693714498513283707353421186155236088813956052327129437629781022749262691591903818002745150640452705864306967771312436295009214557351255495381997105698411916814556536780279272815368148780203872635230392276897038561029968066298918693863362128071013792150689063207647118900886716782643660458005277167365424238794827411411025963471035659129582133847548362840024006275626160743108434783501160707247644258474071101048981371157536016841319724905482389910167999437472868380967163152370362239187926424917469145689563508506504834309075169219014250408812927354102861156064165623878898346687465296913386550602835135798632531680549909595951180893284332783411347133761580603793979970749905619763806933044555810234621000823825742812412350701424826572434253481700878717477193917096525871323813383655618357256914271825408980286254757657357995428L,101679127888134323725416317100411720344826429929601328830868924222029861957243313130888629593943146715504722159868347829741654002116628427240384129016395510386411083515704260057559942172196997688477611541379008440315525316323378006679145918547369295922501238705223385759650387660754808143678545678441899153341228089669541301309154208551196055571665128996579361850190451835989886402761079553669245333442973834901750807859208019800931394134333884538829836559098119575423601453695242340711462656301014871141326221684472998453644674700574750611088468850059788694559149584998461969466200699430608777201007485329143552935271042350737207244773742158476032266489948431865071820745289852064304693461790424825326755826807490144386639668870704391714183649200687936642883542238703444082716114345750431099371235795680332396127429200259296001455589068681502453198015842837674520962582234472173147801727327037498300172851794008303961739725055356570920954996102811127534547751755606626494829801001521950432984882492261314920320540574998939744987184277444447882158088666360204231746334686511237233889476914338775126672202451100099836815620060273259496385106193137702971000898173496712086672858552829708543458356018009228876954328125176399940266486721L,651772959894870840060102038649718098624287975188831353563157895211464117397354692694376307356217104809294356436693017232734414966073515715756220710870282877518135284377272355100684336075930019293411882322079560643529612235963044721844611100622244718471536231327233428643853698908853467079122167042327498402688154226515102711290801517703393081695874935492231825031203363534068625173045722223997882474274748963849884733327551858142505525087203555003800843026732158720251038619039816119396261158977354910621299476774407868591073821412845260844364621190213250892034844436195591940833748984393882432317958987741676458005543046381494570625865553127054568200356516586531928435872450053173532081370638426771798393956893679060639774311468035158208104718372121197462041463810903719442698671063036585602918806277123795224127059383077780909672382158306786154051753779666264201462236110658367733033404001181979613839663302066116787817088037203018689704591027311041019288748853090272606431612223021609997420842480765936764638248845753574667339942415336226419163132243409610852241935411558278958551060715644054460732821982619702657854190398281165478586242902687379449741828444267651003458264204219235283795584568034971205824995190606412406743814912L]
data = zip(c, n)
x, n = CRT(data)
m = gmpy2.iroot(gmpy2.mpz(x), e)[0].digits()
print long_to_bytes(m)
|
注:exp脚本中的n为数组形式表示的多个n的值,中间用逗号隔开。(建议先将n从十六进制转为十进制)。
脚本执行结果:
其中关系式如下:
1
2
|
dp=d%(p-1)
dq=d%(q-1)
|
解题脚本:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
#!/usr/bin/python
#coding:utf-8
import gmpy2
from Crypto.Util.number import long_to_bytes
c = xxx
p = xxx
q = xxx
dp = xxx
dq = xxx
InvQ=gmpy2.invert(q,p)
mp=pow(c,dp,p)
mq=pow(c,dq,q)
m=(((mp-mq)*InvQ)%p)*q+mq
print long_to_bytes(m)
|
这个题型实在没找到对应的题目,就先只记录一下这种方法吧,说不定以后会遇到。
建议先跳过(12)先看后面的(13)(14)…,等时间充裕的时候再回来好好研究这部分。(12)这部分我写的不是很详细,建议看看后去网上找些其他相关的资料进行学习。
之前已经成功安装了 sage,现在我们再来介绍一个工具包RSA-and-LLL-attacks,具体的功能在这个目录中的 ppt 和 pdf 有详细介绍。下载链接:
https://github.com/mimoo/RSA-and-LLL-attacks
适用情况:若 e 较小,并且已知 m 的高位,则可通过此方法求出完整的 m。
什么叫 m 的高位呢,很简单,比如题目给你m=0x65c46754a7776c8b88867e000000000000000000 前面的部分就是高位,后面的 0 就是低位,0 只是占位的作用并不是真正 m 的值。
题目: 13-2019强网杯copperstudy—level1
题目给出如下加密脚本参数:
1
2
3
4
5
|
n=0xa1888c641a05aeb81b3d1686317a86f104791fe1d570a5b11209f45d09ea401d255a70744e7a2d39520e359c23a9f1209ee47f496dbd279e62ee1648b3a277ced8825298274322e0a7a86deea282676310a73b6bb946fc924c34ac6c8784ff559bf9a004c03fb167ef54aaea90ce587f2f3074b40d7f632022ec8fb12e659953L
e=3
m=random.getrandbits(512)
c=pow(m,e,n)=0x93145ece45f416a11e5e9475518f165365456183c361500c2f78aff263028c90f20b7d97205f54e21f3bcc8a556b457889fde3719d0a0f9c9646f3f0d0a1e4bee0f259f023168fe8cc0511848c1635022fcc20b6088084585e2f8055a9d1b1d6bdb228087900bf7c6d42298f8e45c451562c816e2303990834c94e580bf0cbd1L
((m>>72)<<72)=0x9e67d3a220a3dcf6fc4742052621f543b8c78d5d9813e69272e65ac676672446e5c88887e8bfdfc92ec87ec74c16350e6b539e3bd910b000000000000000000L
|
要求出完整的 m 的值。
很明显 e 较小,并且已知了 m 的高位,我们通过 CopperSmith 算法的 Stereotyped messages Attack 获得完整的 m。sage 解题脚本(交互模式):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
load("coppersmith.sage")
N = 0xa1888c641a05aeb81b3d1686317a86f104791fe1d570a5b11209f45d09ea401d255a70744e7a2d39520e359c23a9f1209ee47f496dbd279e62ee1648b3a277ced8825298274322e0a7a86deea282676310a73b6bb946fc924c34ac6c8784ff559bf9a004c03fb167ef54aaea90ce587f2f3074b40d7f632022ec8fb12e659953L
e = 3
m = 0x9e67d3a220a3dcf6fc4742052621f543b8c78d5d9813e69272e65ac676672446e5c88887e8bfdfc92ec87ec74c16350e6b539e3bd910b000000000000000000L
c = 0x93145ece45f416a11e5e9475518f165365456183c361500c2f78aff263028c90f20b7d97205f54e21f3bcc8a556b457889fde3719d0a0f9c9646f3f0d0a1e4bee0f259f023168fe8cc0511848c1635022fcc20b6088084585e2f8055a9d1b1d6bdb228087900bf7c6d42298f8e45c451562c816e2303990834c94e580bf0cbd1L
ZmodN = Zmod(N)
P.<x> = PolynomialRing(ZmodN)
f = (m + x)^e - c
dd = f.degree()
beta = 1
epsilon = beta / 7
mm = ceil(beta**2 / (dd * epsilon))
tt = floor(dd * mm * ((1/beta) - 1))
XX = ceil(N**((beta**2/dd) - epsilon))
roots = coppersmith_howgrave_univariate(f, N, beta, mm, tt, XX)
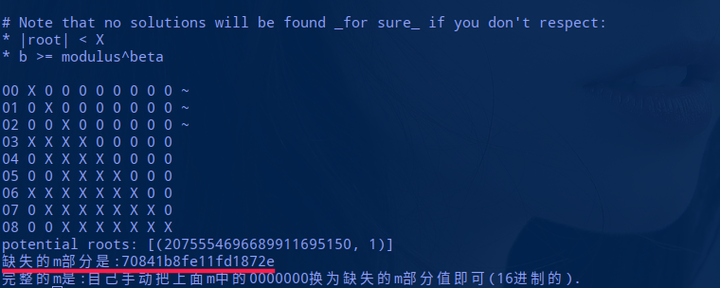
print "缺失的m部分是:"+hex(roots[0])
print "完整的m是:自己手动把上面m中的0000000换为缺失的m部分值即可(16进制的)."
|
sage 是基于python开发,所以 Python 的语法几乎对它完全适用,但是 sage 自己还开发出了很多语法格式和数学公式,学习难度还是不低的,所以我把这些脚本都当做了工具,拿来直接用,自己写出来似乎能力还不够,因为不光要学语法,关键是这里面的数学算法知识。
使用方法:通过终端进入上面说的 RSA-and-LLL-attacks 工具包目录下,然后运行 sage。
复制脚本内容到终端中然后回车回车运行(不知为何无法直接运行脚本,很是不解,可能是我的打开方式不对,你要是会的话,麻烦一定和我说一声,就当是带带我吧)
ps:感谢大佬@啦啦啦 提供的方法 sage下直接运行load(“exp.sage”)就可以解题运行,不用粘贴脚本内容了。
适用情况:若 e 较小,已知 d 的低位,则可通过此方法求出完整的 d。
Partial Key Exposure Attack 中文名叫部分私钥暴露攻击”。
题目: 13-2019强网杯copperstudy—level3
题目给出如下加密脚本参数:
1
2
3
4
5
6
|
n=0x51fb3416aa0d71a430157d7c9853602a758e15462e7c08827b04cd3220c427bbb8199ed4f5393dae43f013b68732a685defc17497f0912c886fa780dfacdfbb1461197d95a92a7a74ade874127a61411e14a901382ed3fb9d62c040c0dbaa374b5a4df06481a26da3fca271429ff10a4fc973b1c82553e3c1dd4f2f37dc24b3bL
e=3
m=random.getrandbits(512)
c=pow(m,e,n)=0x3d7e16fd8b0b1afdb4e12594c3d8590f1175800ef07bb275d7a8ad983d0d5d5fd5c6f81efa40f5d10c48bb200f805e679d633ee584748e5feef003e0921dea736ba91eef72f3d591d3a54cd59fd36f61140fdd3fb2e2c028b684e50cbeae4a1f386f6ab35359d46a29996c0f7d9a4a189f1096150496746f064c3cc41cf111b0L
d=invmod(e,(p-1)*(q-1))
d&((1<<512)-1)=0x17c4b18f1290b6a0886eaa7bf426485a3994c5b71186fe84d5138e18de7e060db57f9580381a917fdfd171bfd159825a7d1e2800e2774f5e4449d17e6723749bL
|
要求出完整的 d。
sage 解题脚本:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
def partial_p(p0, kbits, n):
PR.<x> = PolynomialRing(Zmod(n))
nbits = n.nbits()
f = 2^kbits*x + p0
f = f.monic()
roots = f.small_roots(X=2^(nbits//2-kbits), beta=0.3) # find root < 2^(nbits//2-kbits) with factor >= n^0.3
if roots:
x0 = roots[0]
p = gcd(2^kbits*x0 + p0, n)
return ZZ(p)
def find_p(d0, kbits, e, n):
X = var('X')
for k in xrange(1, e+1):
results = solve_mod([e*d0*X - k*X*(n-X+1) + k*n == X], 2^kbits)
for x in results:
p0 = ZZ(x[0])
p = partial_p(p0, kbits, n)
if p:
return p
if __name__ == '__main__':
# n(必须为整形才可计算) = 0x51fb3416aa0d71a430157d7c9853602a758e15462e7c08827b04cd3220c427bbb8199ed4f5393dae43f013b68732a685defc17497f0912c886fa780dfacdfbb1461197d95a92a7a74ade874127a61411e14a901382ed3fb9d62c040c0dbaa374b5a4df06481a26da3fca271429ff10a4fc973b1c82553e3c1dd4f2f37dc24b3bL
# d0=给出的部分d(必须为整形才可计算) = 0x17c4b18f1290b6a0886eaa7bf426485a3994c5b71186fe84d5138e18de7e060db57f9580381a917fdfd171bfd159825a7d1e2800e2774f5e4449d17e6723749bL
e = 3
n = 57569201048993475052349187244752169754165154575782760003851777813767048953051839288528137121670999884309849815765999616346303792471518639080697166767644957046582385785721102370288806038187956032505761532789716009522131450217010629338000241936036185205038814391205848232364006349213836317806903032515194407739
nbits = n.nbits()
kbits = floor(nbits*0.5)
print "kbits : ", kbits
d0 = 1244848677959253796774387650148978357579294769878147704641867595620534030329181934099194560059806799908134954814673426128260540575360296026444649631806619
print "lower %d bits (of %d bits) is given" % (kbits, nbits)
p = find_p(d0, kbits, e, n)
print "found p: %d" % p
q = n//p
# print d
print "完整的d是:"+str(inverse_mod(e, (p-1)))
|
脚本注释:d0 代表已知的 d 的较低位,kbits 是已知的 d0 的位数。
题目: 13-2019强网杯copperstudy—level2
题目给出如下加密脚本参数:
1
2
3
4
5
|
n=0x241ac918f708fff645d3d6e24315e5bb045c02e788c2b7f74b2b83484ce9c0285b6c54d99e2a601a386237d666db2805175e7cc86a733a97aeaab63486133103e30c1dca09741819026bd3ea8d08746d1d38df63c025c1793bdc7e38d194a30b492aadf9e31a6c1240a65db49e061b48f1f2ae949ac9e7e0992ed24f9c01578dL
e=65537
m=random.getrandbits(512)
c=pow(m,e,n)=0x1922e7151c779d6bb554cba6a05858415e74739c36df0bcf169e49ef0e566a4353c51a306036970005f2321d1d104f91a673f40944e830619ed683d8f84eaf26e7a93c4abe1dbd7ca3babf3f4959def0e3d87f7818d54633a790fc74e9fed3c5b5456c21e3f425240f6217b0b14516cb59aa0ce74b83ca17d8cc4a0fbc829fb8L
((p>>128)<<128)=0x2c1e75652df018588875c7ab60472abf26a234bc1bfc1b685888fb5ded29ab5b93f5105c1e9b46912368e626777a873200000000000000000000000000000000L
|
要求完整的 p。
sage 解题脚本:
1
2
3
4
5
6
7
8
9
10
11
12
13
|
n = 0x241ac918f708fff645d3d6e24315e5bb045c02e788c2b7f74b2b83484ce9c0285b6c54d99e2a601a386237d666db2805175e7cc86a733a97aeaab63486133103e30c1dca09741819026bd3ea8d08746d1d38df63c025c1793bdc7e38d194a30b492aadf9e31a6c1240a65db49e061b48f1f2ae949ac9e7e0992ed24f9c01578dL
p_fake = 0x2c1e75652df018588875c7ab60472abf26a234bc1bfc1b685888fb5ded29ab5b93f5105c1e9b46912368e626777a873200000000000000000000000000000000L
pbits = 1024
kbits = 130
pbar = p_fake & (2^pbits-2^kbits)
print "upper %d bits (of %d bits) is given" % (pbits-kbits, pbits)
PR.<x> = PolynomialRing(Zmod(n))
f = x + pbar
x0 = f.small_roots(X=2^kbits, beta=0.4)[0] # find root < 2^kbits with factor >= n^0.3
print hex(int(x0 + pbar))
|
题目内容如下:

解题脚本:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
#!/usr/bin/python
#coding:utf-8
import gmpy2
import libnum
from Crypto.Util.number import long_to_bytes
e= 65537
n = 9637571466652899741848142654451413405801976834328667418509217149503238513830870985353918314633160277580591819016181785300521866901536670666234046521697590230079161867282389124998093526637796571100147052430445089605759722456767679930869250538932528092292071024877213105462554819256136145385237821098127348787416199401770954567019811050508888349297579329222552491826770225583983899834347983888473219771888063393354348613119521862989609112706536794212028369088219375364362615622092005578099889045473175051574207130932430162265994221914833343534531743589037146933738549770365029230545884239551015472122598634133661853901
c = 5971372776574706905158546698157178098706187597204981662036310534369575915776950962893790809274833462545672702278129839887482283641996814437707885716134279091994238891294614019371247451378504745748882207694219990495603397913371579808848136183106703158532870472345648247817132700604598385677497138485776569096958910782582696229046024695529762572289705021673895852985396416704278321332667281973074372362761992335826576550161390158761314769544548809326036026461123102509831887999493584436939086255411387879202594399181211724444617225689922628790388129032022982596393215038044861544602046137258904612792518629229736324827
dp = 81339405704902517676022188908547543689627829453799865550091494842725439570571310071337729038516525539158092247771184675844795891671744082925462138427070614848951224652874430072917346702280925974595608822751382808802457160317381440319175601623719969138918927272712366710634393379149593082774688540571485214097
for i in range(1,65538):
if (dp*e-1)%i == 0:
if n%(((dp*e-1)/i)+1)==0:
p=((dp*e-1)/i)+1
q=n/(((dp*e-1)/i)+1)
phi = (p-1)*(q-1)
d = gmpy2.invert(e,phi)%phi
m = pow(c,d,n)
print long_to_bytes(m)
|
适用情况:题目给出的模数 N 可直接分解,但是分解之后得到了多个不同的因子
题目: 15-山东省大学生爱好者线上赛-上午RSA
题目给出一个文件里面的内容如下:
1
2
3
4
|
n= 544187306850902797629107353619267427694837163600853983242783
e= 39293
c= 439254895818320413408827022398053685867343267971712332011972
m=???
|
很明显 n 不大,可直接使用 factordb 进行分解。

分解得到了三个因子,其实当时做这题时我也是一脸懵的,从没遇到过,试了 n 种方法,最后推到了这个方法。
解题脚本如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
#!/usr/bin/python
#coding:utf-8
import gmpy2
from Crypto.Util.number import long_to_bytes
n= 544187306850902797629107353619267427694837163600853983242783
e= 39293
c= 439254895818320413408827022398053685867343267971712332011972
p1 = 67724172605733871
p2 = 11571390939636959887
p3 = 694415063702720454699679
phi = (p1-1)*(p2-1)*(p3-1)
d = gmpy2.invert(e, phi)
m = pow(c, d, n)
print long_to_bytes(m)
|
适用情况:可以通过选择输入的密文进而泄露最低位解题。
该攻击方式详细请参考该文章:
https://introspelliam.github.io/2018/03/27/crypto/RSA-Least-Significant-Bit-Oracle-Attack/
题目: 14-SUCTF-RSA
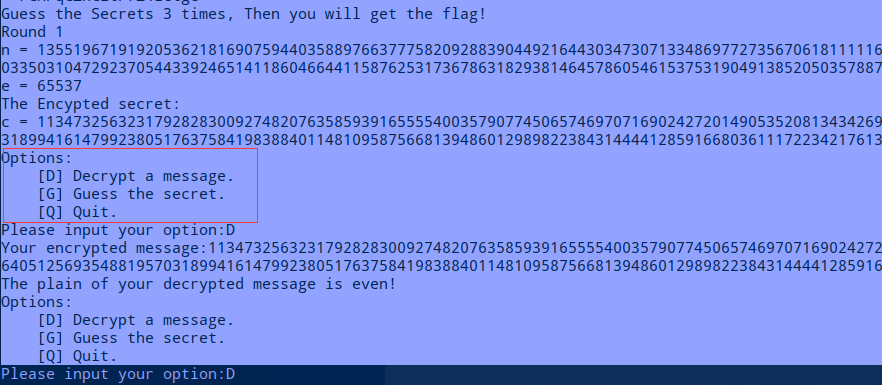

正式进入 rsa 解题之前会让你提供一个字符串 str,只有 md5(str+给定的值salt) == 给定的部分哈希值 part_hash,才能进入正式的题目。
然后,通过输入D,服务端会帮你解给出的给出的密文,但只会返回这个数是奇数(odd)还是偶数(even),通过G选项可以测试你输入的m是否正确,如果正确就会进入下1轮的
解题(三轮都是相同的原理,只是给出数c,n不同)(必须使用交互式解题)
解题脚本:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
|
from pwn import *
from hashlib import md5
import decimal
a = 0
def oracle(num):
p.recvuntil("Please input your option:")
p.sendline("D")
p.recvuntil("Your encrypted message:")
p.sendline(str(num))
p.recvuntil("The plain of your decrypted message is ")
lsb = p.recv(3)
return lsb == 'odd'
def partial(c,e,n):
k = n.bit_length()
decimal.getcontext().prec = k # for 'precise enough' floats
lo = decimal.Decimal(0)
hi = decimal.Decimal(n)
for i in range(k):
if not oracle(c):
hi = (lo + hi) / 2
else:
lo = (lo + hi) / 2
c = (c * pow(2, e, n)) % n
print i, int(hi - lo)
return int(hi)
s = "0123456789abcdefABCDEF"
p = remote("127.0.0.1","9991")
p.recvuntil("[*] Please find a string that md5(str + ")
salt = p.recv(4)
p.recvuntil("[0:5] == ")
part_hash = p.recv(5)
found = 0
for i in s:
for j in s:
for k in s:
for l in s:
for m in s:
ss = i+j+k+l+m
if md5(ss+salt).hexdigest()[:5] == part_hash:
found = 1
break
if found:
break
if found:
break
if found:
break
if found:
break
p.recvuntil("> ")
p.sendline(ss)
p.recvuntil("Guess the Secrets 3 times, Then you will get the flag!\n")
for i in range(3):
R = p.recvline().strip()
p.recvuntil("n = ")
n = eval(p.recvline().strip())
p.recvuntil("e = ")
e = eval(p.recvline().strip())
p.recvuntil("The Encypted secret:")
p.recvuntil("c = ")
c = eval(p.recvline().strip())
c_of_2 = pow(2,e,n)
m = partial((c*c_of_2)%n,e,n)
p.recvuntil("Please input your option:")
p.sendline("G")
p.recvuntil('The secret:')
p.sendline(str(m))
s = p.recvline().strip()
print(s)
log.success(s+' '+R+" success!")
p.interactive()
|
本题摘自Nu1L战队的wp。
西湖论剑2020–BrokenSystems。
题目给出三个文件,一个加密脚本 BrokenSystems.py,一个密文文件 message,一个 RSA 公钥文件 public.key。

通过 openssl 查看,可以看到该公钥文件的e特别大,此时便存在 rsa-wiener-attack 攻击,通过此可以求出 d。
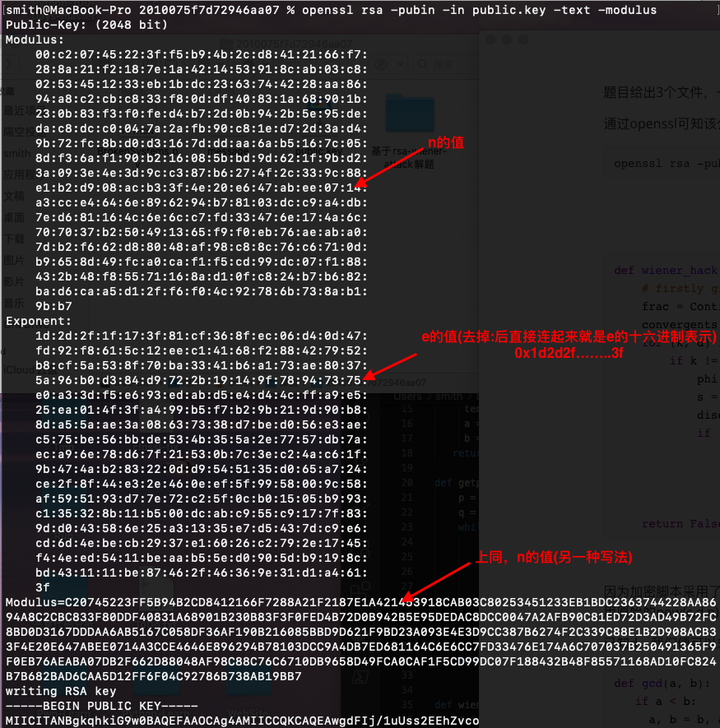
通过 rsa-wiener-attack 求解 d:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
from Crypto.PublicKey import RSA
import ContinuedFractions, Arithmetic
def wiener_hack(e, n):
# firstly git clone https://github.com/pablocelayes/rsa-wiener-attack.git !
frac = ContinuedFractions.rational_to_contfrac(e, n)
convergents = ContinuedFractions.convergents_from_contfrac(frac)
for (k, d) in convergents:
if k != 0 and (e * d - 1) % k == 0:
phi = (e * d - 1) // k
s = n - phi + 1
discr = s * s - 4 * n
if (discr >= 0):
t = Arithmetic.is_perfect_square(discr)
if t != -1 and (s + t) % 2 == 0:
print("First: Hacked d.")
return d
return False
n = 0xC20745223FF5B94B2CD8412166F7288A21F2187E1A421453918CAB03C80253451233EB1BDC2363744228AA8694A8C2CBC833F80DDF40831A68901B230B83F3F0FED4B72D0B942B5E95DEDAC8DCC0047A2AFB90C81ED72D3AD49B72FC8BD0D3167DDDAA6AB5167C058DF36AF190B216085BBD9D621F9BD23A093E4E3D9CC387B6274F2C339C88E1B2D908ACB33F4E20E647ABEE0714A3CCE4646E896294B78103DCC9A4DB7ED681164C6E6CC7FD33476E174A6C707037B250491365F9F0EB76AEABA07DB2F662D88048AF98C88C76C6710DB9658D49FCA0CAF1F5CD99DC07F188432B48F85571168AD10FC824B7B682BAD6CAA5D12FF6F04C92786B738AB19BB7
e = 0x1d2d2f1f173f81cf368fec06d40d47fd92f8615c12eec14168f288427952b8cf5a538f70ba3341b6a173ae80375a96b0d384d9722b19149f78947375e0a33df5e693edabd5e4d44cffa9e525ea014f3fa499b5f7b29b219d90b88da55aae3a08637338d7bed056e3aec575be56bbde534b355a2e7757db7aeca96e78d67f21530b7c3ec24ac61f9b474ab283220dd9545135d065a724ce2f8f44e32e460eef5f9958009c58af595193d77e72c25f0cb01505b993c135328b11b500dcabc955c9177f839dd043586e25a31335e7d5437dc9e6cd6d4ebecb2937e16026c2792e1745f44eed5411beaab55ed0905db9198cbd431111be87462f46369e31d1a4613f
message = open('./message', 'r')
secret = message.read()
d = wiener_hack(e, n)
|
此时,我们便可以求出 d。已知 d,我们便可以求出 p 和 q。
1
2
3
4
5
6
7
8
9
10
11
12
13
|
def getpq(n,e,d):
p = 1
q = 1
while p==1 and q==1:
k = d * e - 1
g = random.randint ( 0 , n )
while p==1 and q==1 and k % 2 == 0:
k /= 2
y = pow(g,k,n)
if y!=1 and gcd(y-1,n)>1:
p = gcd(y-1,n)
q = n/p
return p,q
|
因为加密脚本采用了 PKCS1_OAEP 模式下的 RSA 加密,所以我们需要通过手动构造私钥进而才可以去解密密文。采用原始的 pow(c,d,n) 是无法正确的解密密文的。
因此,我们需要先采用 PKCS1_OAEP 模式构造私钥,然后利用这个私钥来解密密文文件。
1
2
3
4
5
|
privkey = RSA.construct((long(n), long(e), long(d), long(p), long(q)))
key = PKCS1_OAEP.new(privkey)
m = key.decrypt(secret)
print m
|
完整的 exp 如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
|
#rsa-wiener-attack/exp1.py
#!/usr/bin/python
#coding:utf-8
import gmpy2
import random
from Crypto.PublicKey import RSA
import ContinuedFractions, Arithmetic
from Crypto.Cipher import PKCS1_OAEP
from Crypto.Util.number import long_to_bytes
def gcd(a, b):
if a < b:
a, b = b, a
while b != 0:
temp = a % b
a = b
b = temp
return a
def getpq(n,e,d):
p = 1
q = 1
while p==1 and q==1:
k = d * e - 1
g = random.randint ( 0 , n )
while p==1 and q==1 and k % 2 == 0:
k /= 2
y = pow(g,k,n)
if y!=1 and gcd(y-1,n)>1:
p = gcd(y-1,n)
q = n/p
return p,q
def wiener_hack(e, n):
# firstly git clone https://github.com/pablocelayes/rsa-wiener-attack.git !
frac = ContinuedFractions.rational_to_contfrac(e, n)
convergents = ContinuedFractions.convergents_from_contfrac(frac)
for (k, d) in convergents:
if k != 0 and (e * d - 1) % k == 0:
phi = (e * d - 1) // k
s = n - phi + 1
discr = s * s - 4 * n
if (discr >= 0):
t = Arithmetic.is_perfect_square(discr)
if t != -1 and (s + t) % 2 == 0:
print("First: Hacked d.")
return d
return False
def main():
n = 0xC20745223FF5B94B2CD8412166F7288A21F2187E1A421453918CAB03C80253451233EB1BDC2363744228AA8694A8C2CBC833F80DDF40831A68901B230B83F3F0FED4B72D0B942B5E95DEDAC8DCC0047A2AFB90C81ED72D3AD49B72FC8BD0D3167DDDAA6AB5167C058DF36AF190B216085BBD9D621F9BD23A093E4E3D9CC387B6274F2C339C88E1B2D908ACB33F4E20E647ABEE0714A3CCE4646E896294B78103DCC9A4DB7ED681164C6E6CC7FD33476E174A6C707037B250491365F9F0EB76AEABA07DB2F662D88048AF98C88C76C6710DB9658D49FCA0CAF1F5CD99DC07F188432B48F85571168AD10FC824B7B682BAD6CAA5D12FF6F04C92786B738AB19BB7
e = 0x1d2d2f1f173f81cf368fec06d40d47fd92f8615c12eec14168f288427952b8cf5a538f70ba3341b6a173ae80375a96b0d384d9722b19149f78947375e0a33df5e693edabd5e4d44cffa9e525ea014f3fa499b5f7b29b219d90b88da55aae3a08637338d7bed056e3aec575be56bbde534b355a2e7757db7aeca96e78d67f21530b7c3ec24ac61f9b474ab283220dd9545135d065a724ce2f8f44e32e460eef5f9958009c58af595193d77e72c25f0cb01505b993c135328b11b500dcabc955c9177f839dd043586e25a31335e7d5437dc9e6cd6d4ebecb2937e16026c2792e1745f44eed5411beaab55ed0905db9198cbd431111be87462f46369e31d1a4613f
message = open('./message', 'r')
secret = message.read()
d = wiener_hack(e, n)
p,q = getpq(n,e,d)
#print p
#print q
privkey = RSA.construct((long(n), long(e), long(d), long(p), long(q)))
key = PKCS1_OAEP.new(privkey)
m = key.decrypt(secret)
print m
if __name__=="__main__":
main()
|
注意,该脚本需要rsa-wiener-attack工具包的目录中执行,还需提前将密文文件message一同放到该目录下。
解题脚本如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
|
#!/usr/bin/python
#coding:utf-8
import gmpy2
import random
from Crypto.PublicKey import RSA
import ContinuedFractions, Arithmetic
from Crypto.Cipher import PKCS1_OAEP
from Crypto.Util.number import long_to_bytes
def gcd(a, b):
if a < b:
a, b = b, a
while b != 0:
temp = a % b
a = b
b = temp
return a
def getpq(n,e,d):
p = 1
q = 1
while p==1 and q==1:
k = d * e - 1
g = random.randint ( 0 , n )
while p==1 and q==1 and k % 2 == 0:
k /= 2
y = pow(g,k,n)
if y!=1 and gcd(y-1,n)>1:
p = gcd(y-1,n)
q = n/p
return p,q
def wiener_hack(e, n):
# firstly git clone https://github.com/pablocelayes/rsa-wiener-attack.git !
frac = ContinuedFractions.rational_to_contfrac(e, n)
convergents = ContinuedFractions.convergents_from_contfrac(frac)
for (k, d) in convergents:
if k != 0 and (e * d - 1) % k == 0:
phi = (e * d - 1) // k
s = n - phi + 1
discr = s * s - 4 * n
if (discr >= 0):
t = Arithmetic.is_perfect_square(discr)
if t != -1 and (s + t) % 2 == 0:
print("First: Hacked d.")
return d
return False
def main():
n = 0xC20745223FF5B94B2CD8412166F7288A21F2187E1A421453918CAB03C80253451233EB1BDC2363744228AA8694A8C2CBC833F80DDF40831A68901B230B83F3F0FED4B72D0B942B5E95DEDAC8DCC0047A2AFB90C81ED72D3AD49B72FC8BD0D3167DDDAA6AB5167C058DF36AF190B216085BBD9D621F9BD23A093E4E3D9CC387B6274F2C339C88E1B2D908ACB33F4E20E647ABEE0714A3CCE4646E896294B78103DCC9A4DB7ED681164C6E6CC7FD33476E174A6C707037B250491365F9F0EB76AEABA07DB2F662D88048AF98C88C76C6710DB9658D49FCA0CAF1F5CD99DC07F188432B48F85571168AD10FC824B7B682BAD6CAA5D12FF6F04C92786B738AB19BB7
e = 0x1d2d2f1f173f81cf368fec06d40d47fd92f8615c12eec14168f288427952b8cf5a538f70ba3341b6a173ae80375a96b0d384d9722b19149f78947375e0a33df5e693edabd5e4d44cffa9e525ea014f3fa499b5f7b29b219d90b88da55aae3a08637338d7bed056e3aec575be56bbde534b355a2e7757db7aeca96e78d67f21530b7c3ec24ac61f9b474ab283220dd9545135d065a724ce2f8f44e32e460eef5f9958009c58af595193d77e72c25f0cb01505b993c135328b11b500dcabc955c9177f839dd043586e25a31335e7d5437dc9e6cd6d4ebecb2937e16026c2792e1745f44eed5411beaab55ed0905db9198cbd431111be87462f46369e31d1a4613f
message = open('./message', 'r')
secret = message.read()
d = wiener_hack(e, n)
p,q = getpq(n,e,d)
#print p
#print q
privkey = RSA.construct((long(n), long(e), long(d), long(p), long(q)))
key = PKCS1_OAEP.new(privkey)
m = key.decrypt(secret)
print m
if __name__=="__main__":
main()
|

以上是我当时做的步骤。
大佬们其实只要几行代码就可以解决,膜膜膜。
以下是 ChaMd5 团队给出的本题 WriteUp(我进行了部分修改,便于理解):
维纳攻击,公钥文件中获取到 e 很大,利用维纳攻击可以拿到 d。
维纳攻击:https://github.com/pablocelayes/rsa-wiener-attack
然后利用 e、d、n 获取 p、q,生成私钥文件:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
#exp2.py
from Crypto.PublicKey import RSA
from Crypto.Util.number import inverse, long_to_bytes
e = 3683191938452247871641914583009119792552938079110383367782698429399084083048335018186915282465581498846777124014232879019914546010406868697694661244001972931366227108140590201194336470785929194895915077935083045957890179080332615291089360169761324533970721460473221959270664692795701362942487885620152952927112838769014944652059440137350285198702402612151501564899791870051001152984815689187374906618917967106000628810361686645504356294175173529719443860140795170776862320812544438211122891112138748710073230404456268507750721647637959502454394140328030018450883598342764577147457231373121223878829298942493059211583
d = 1779217788383673416690068487595062922771414230914791138743960472798057054853883175313487137767631446949382388070798609545617543049566741624609996040273727
n = 24493816160588971749455534346389861269947121809901305744877671102517333076424951483888863597563544011725032585417200878377314372325231470164799594965293350352923195632229495874587039720317200655351788887974047948082357232348155828924230567816817425104960545706688263839042183224681231800805037117758927837949941052360649778743187012198508745207332696876463490071925421229447425456903529626946628855874075846839745388326224970202749994059533831664092151570836853681204646481502222112116971464211748086292930029540995987019610460396057955900244074999111267618452967579699626655472948383601391620012180211885979095636919
p=163724217068973025857079545677048587508164102644298632911494474022224582218067057349189211462632427829087720476013052665037199232658015194718500750961261016558605363103092187533086949903145449057015220561698195502163792192055762108803714387175594231859738263839090338762578040513451585421537323416472060788989
q=149604112324264915811376746906108325951188179904814259006959765070266946659481820938211689946210254302179197289522748397160602946376246768419310765669852537378426700376878745285639531531077237124655345323906476180103106894642043615024716862503414785057646920410083538192951872861366496901158348770066798098371
keypair = RSA.generate(2048)
keypair.p = p
keypair.q = q
keypair.e = e
keypair.n = n
keypair.d = d
private_key = keypair.exportKey().decode('utf-8')
f = open('pri.pem', 'w') #生成的私钥文件是pri.pem。
f.write(private_key)
|
openssl 解密即可。
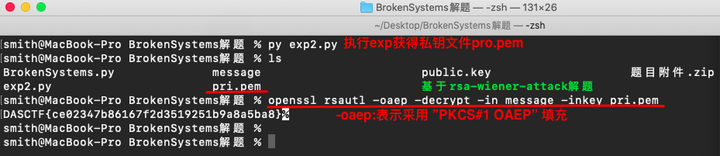
详细的openssl使用方法可参考:
https://abcdxyzk.github.io/blog/2018/02/09/tools-openssl/
题目给出 p+q,(p+1)(q+1),e 和 c。

首先需要求出 phi,然后求解 d,最后再求解 m。
1
2
|
phi = (p-1)(q-1)
= pq - (p+q) + 1
|
p+q 的值题目已经给出了,接下来只需要求出 pq 的值即可求出 phi 的值。题目还给出了 (p+1)(q+1),我们考虑下 pq 是否可以表示为 (p+1)(q+1) 的形式:
1
2
|
(p+1)(q+1) = pq + p + q + 1
= pq + (p+q) + 1
|
那么 pq 就可以表示为:
1
|
pq = (p+1)(q+1) - (p+q) -1
|
然后,求解 phi 的值。
1
2
3
|
phi = (p-1)(q-1)
= pq - (p+q) + 1
= n - (p+q) + 1
|
最后:
1
2
|
d = gmpy2.invert(e,phi)
m = pow(c,d,n)
|
完整的解题脚本如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
#!/usr/bin/python
#coding:utf-8
import gmpy2
from Crypto.Util.number import long_to_bytes
#p+q通过p_add_q表示
p_add_q = 326429100407681651814978442415826213864753565034919374282004148849764531414964129530662174521568050093736341197400405816551402307458686750141836996345723514698979514133066389538988520826440776264241138888155090851605191090286605183976443204444854546781116840786281855819689375353337207819361769484061133586660
#(p+1)(q+1)为了方便用x表示
x = 26601616557971867831128918184476970808722471200861600741488181559976427915212193001812160532906370924454473038671991616741424706794741682437728013348910646937734672343325523407437596920797247711273378236903138971315823251358525257853681659038646150834388504990678755552658405772625078429891153401221091704935464031276762725209220275197422069811202440482709667987828399235771854454331605660739185369563297937712412914621262089799368586352843414856752338979163598254668715003106493342377951882955338211218066635494610164992383277776336257215001515405312235576928828485922034700150519853591032361405975195251746299510720
c = 24831377919906161196266552704492935537768087456188711284519872226691826290351027606307936414989585764319104737516021733938210516424254235349369088344349700976416957839221585194510124601438798302079231278339823353520868327987552051471031155633165987892206927171527428590536203275545528900845222038924459888879261986663709510987273937159905675940592632023428129764650249246182611973968609631056274792336171105433760493214971141615401120748113420469659787315651721605227003326305005720436114240966565179896456348773794946970503274768701856591123183247406604013805700201562056023223765073732621940021232679124486597812994
e = 65537
#n = pq = (p+1)(q+1) - (p+q) - 1 = x - p_add_q - 1
n = x - p_add_q - 1
#phi = (p-1)(q-1) = pq - (p+q) + 1 = n - (p+q) + 1 = n - p_add_q + 1
phi = n - p_add_q + 1
d = gmpy2.invert(e,phi)
m = pow(c,d,n)
print(long_to_bytes(m))
|
运行结果:

这个题相比于(17)而言,不太容易直接想到转化的等式。
题目给出 p-q,n,e 和 c。

常规的 RSA 解密步骤:
1
2
3
4
|
n = p*q
phi = (p-1)*(q-1)
d = gmpy2.invert(e,phi)
m = pow(c,d,n)
|
因为 n 不可分解,所以,我们无法直接得到 p 和 q 的值,也就无法得到 phi 的值。
通过对 phi 的如下分解可知,如果已知 n 和 p+q 便可求得 phi 的值。
1
2
3
|
phi = (p-1)*(q-1)
= p*q - (p+q) + 1
= n - (p+q) + 1
|
因为,给了 p-q 的值,所以,我们需要设法将 p+q 表示为 p-q,进而求得 phi 的值。
推导过程如下:
(1) p-q 的平方可以如下分解:
$$
(p-q)^2 = p^2 + q^2 -2pq
$$
因此:
$$
p^2 + q^2 = (p-q)^2 +2pq
$$
(2) p+q 的平方可以如下分解:
$$
\begin{aligned}
(p+q)^2
&= p^2 + q^2 + 2pq \\
&= (p-q)^2 + 2pq + 2pq \\
&= (p-q)^2 + 4pq
\end{aligned}
$$
故 p+q 可表示为:
$$
\begin{aligned} p+q
&= \sqrt{(p-q)^2 + 4pq} \\
&= \sqrt{(p-q)^2 + 4n}
\end{aligned}
$$
这样,我们就可以求出 p+q 的值,进而可以求出 phi 的值。最后就可以求出明文 m 的值了。
解题脚本如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
#!/usr/bin/python
#coding:utf-8
#变量p_add_q:p + q
#变量p_sub_q:p - q
import gmpy2
from Crypto.Util.number import long_to_bytes
n = 27552304606229034903366058815849954030287648695063385362955432137790872571412035824128918674719247737295565001575991597519270789776408208970323808016733976338433371328100880898942106515627607388226912870981180215883273805491209461671730377099185278711453949265641966582563910708529619185885928310168288810488784242368160743359666583499117949407921812317700250240067929572558785431071173411100434109661677786734923283679392823901052633992456780285091988542875991410528415886437666510014123352497264017734716859350294159440761760921548702546470902740121962033241003215821780125194400741190925169397917247376657863011603
e = 65537
c = 8643831704675414121804983915084443744489969712473300784256427784417167322852556975560503484179280700293119974607254037642425650493676448134024809335297135239994950178868535219541095694358323044214971760829173918774094415933808417722001811285178546917655837402000771685507972240389565704149610032767242977174132826100177368764169367458684152505611469248099487912367364804360878611296860803835816266114046682291529593099394952245852157119233687981777202751472502060481232341206366584532964027749320641690448228420342308891797513656897566100268729012788419021059054907653832828437666012596894150751431936476816983845357
p_sub_q = 3216514606297172806828066063738105740383963382396892688569683235383985567043193404185955880509592930874764682428425994713750665248099953457550673860782324431970917492727256948066013701406000049963109681898567026552657377599263519201715733179565306750754520746601394738797021362510415215113118083969304423858
p_add_q = gmpy2.iroot(p_sub_q**2 + 4*n, 2)
#iroot()返回值为一个(x,y)元组。其中x为结果值,y为一个bool型变量,如果x为整数,y=True,否则y=False。
phi = n - p_add_q[0] + 1
d = gmpy2.invert(e,phi)
m = pow(c,d,n)
print(long_to_bytes(m))
|
运行结果:

综合题目,我就不搬上来了,本质就是这种前面提到的 RSA 题型的套娃,可以访问这个github地址去查看。建议做做里面的题目"V&N2020 公开赛"和"DASCTF题目"。
https://github.com/Mr-Aur0ra/RSA/tree/master/%E7%BB%BC%E5%90%88%E9%A2%98%E7%9B%AE








































